Esta página foi traduzida pela API Cloud Translation.

Diferenciação automática avançada

Veja no TensorFlow.org

Executar no Google Colab

Ver fonte no GitHub

Baixar caderno

O guia Introdução aos gradientes e diferenciação automática inclui tudo o que é necessário para calcular gradientes no TensorFlow. Este guia se concentra em recursos mais profundos e menos comuns da API tf.GradientTape .

Configurar

import tensorflow as tf

import matplotlib as mpl
import matplotlib.pyplot as plt

mpl.rcParams['figure.figsize'] = (8, 6)

Controlando a gravação de gradiente

No guia de diferenciação automática você viu como controlar quais variáveis e tensores são observados pela fita enquanto constrói o cálculo do gradiente.

A fita também tem métodos para manipular a gravação.

Pare de gravar

Se você deseja parar de gravar gradientes, você pode usar tf.GradientTape.stop_recording para suspender temporariamente a gravação.

Isso pode ser útil para reduzir a sobrecarga se você não quiser diferenciar uma operação complicada no meio do seu modelo. Isso pode incluir o cálculo de uma métrica ou um resultado intermediário:

x = tf.Variable(2.0)
y = tf.Variable(3.0)

with tf.GradientTape() as t:
  x_sq = x * x
  with t.stop_recording():
    y_sq = y * y
  z = x_sq + y_sq

grad = t.gradient(z, {'x': x, 'y': y})

print('dz/dx:', grad['x'])  # 2*x => 4
print('dz/dy:', grad['y'])

dz/dx: tf.Tensor(4.0, shape=(), dtype=float32)
dz/dy: None

Redefinir/iniciar a gravação do zero

Se você deseja recomeçar completamente, use tf.GradientTape.reset . Simplesmente sair do bloco de fita gradiente e reiniciar geralmente é mais fácil de ler, mas você pode usar o método de reset quando sair do bloco de fita for difícil ou impossível.

x = tf.Variable(2.0)
y = tf.Variable(3.0)
reset = True

with tf.GradientTape() as t:
  y_sq = y * y
  if reset:
    # Throw out all the tape recorded so far.
    t.reset()
  z = x * x + y_sq

grad = t.gradient(z, {'x': x, 'y': y})

print('dz/dx:', grad['x'])  # 2*x => 4
print('dz/dy:', grad['y'])

dz/dx: tf.Tensor(4.0, shape=(), dtype=float32)
dz/dy: None

Pare o fluxo de gradiente com precisão

Em contraste com os controles globais de fita acima, a função tf.stop_gradient é muito mais precisa. Ele pode ser usado para impedir que gradientes fluam ao longo de um caminho específico, sem precisar acessar a própria fita:

x = tf.Variable(2.0)
y = tf.Variable(3.0)

with tf.GradientTape() as t:
  y_sq = y**2
  z = x**2 + tf.stop_gradient(y_sq)

grad = t.gradient(z, {'x': x, 'y': y})

print('dz/dx:', grad['x'])  # 2*x => 4
print('dz/dy:', grad['y'])

dz/dx: tf.Tensor(4.0, shape=(), dtype=float32)
dz/dy: None

Gradientes personalizados

Em alguns casos, você pode querer controlar exatamente como os gradientes são calculados em vez de usar o padrão. Essas situações incluem:

Não há gradiente definido para uma nova operação que você está escrevendo.
Os cálculos padrão são numericamente instáveis.
Você deseja armazenar em cache um cálculo caro da passagem direta.
Você deseja modificar um valor (por exemplo, usando tf.clip_by_value ou tf.math.round ) sem modificar o gradiente.

Para o primeiro caso, para escrever uma nova operação, você pode usar tf.RegisterGradient para configurar a sua própria (consulte a documentação da API para obter detalhes). (Observe que o registro de gradiente é global, portanto, altere-o com cuidado.)

Para os três últimos casos, você pode usar tf.custom_gradient .

Aqui está um exemplo que aplica tf.clip_by_norm ao gradiente intermediário:

# Establish an identity operation, but clip during the gradient pass.
@tf.custom_gradient
def clip_gradients(y):
  def backward(dy):
    return tf.clip_by_norm(dy, 0.5)
  return y, backward

v = tf.Variable(2.0)
with tf.GradientTape() as t:
  output = clip_gradients(v * v)
print(t.gradient(output, v))  # calls "backward", which clips 4 to 2

tf.Tensor(2.0, shape=(), dtype=float32)

Consulte os documentos da API do decorador tf.custom_gradient para obter mais detalhes.

Gradientes personalizados em SavedModel

Gradientes personalizados podem ser salvos em SavedModel usando a opção tf.saved_model.SaveOptions(experimental_custom_gradients=True) .

Para ser salva no SavedModel, a função gradiente deve ser rastreável (para saber mais, confira o guia Melhor desempenho com tf.function ).

class MyModule(tf.Module):

  @tf.function(input_signature=[tf.TensorSpec(None)])
  def call_custom_grad(self, x):
    return clip_gradients(x)

model = MyModule()

tf.saved_model.save(
    model,
    'saved_model',
    options=tf.saved_model.SaveOptions(experimental_custom_gradients=True))

# The loaded gradients will be the same as the above example.
v = tf.Variable(2.0)
loaded = tf.saved_model.load('saved_model')
with tf.GradientTape() as t:
  output = loaded.call_custom_grad(v * v)
print(t.gradient(output, v))

INFO:tensorflow:Assets written to: saved_model/assets
tf.Tensor(2.0, shape=(), dtype=float32)

Uma observação sobre o exemplo acima: Se você tentar substituir o código acima por tf.saved_model.SaveOptions(experimental_custom_gradients=False) , o gradiente ainda produzirá o mesmo resultado no carregamento. A razão é que o registro de gradiente ainda contém o gradiente personalizado usado na função call_custom_op . No entanto, se você reiniciar o tempo de execução após salvar sem gradientes personalizados, a execução do modelo carregado sob o tf.GradientTape lançará o erro: LookupError: No gradient defined for operation 'IdentityN' (op type: IdentityN) .

Várias fitas

Várias fitas interagem perfeitamente.

Por exemplo, aqui cada fita observa um conjunto diferente de tensores:

x0 = tf.constant(0.0)
x1 = tf.constant(0.0)

with tf.GradientTape() as tape0, tf.GradientTape() as tape1:
  tape0.watch(x0)
  tape1.watch(x1)

  y0 = tf.math.sin(x0)
  y1 = tf.nn.sigmoid(x1)

  y = y0 + y1

  ys = tf.reduce_sum(y)

tape0.gradient(ys, x0).numpy()   # cos(x) => 1.0

1.0

tape1.gradient(ys, x1).numpy()   # sigmoid(x1)*(1-sigmoid(x1)) => 0.25

0.25

Gradientes de ordem superior

As operações dentro do gerenciador de contexto tf.GradientTape são registradas para diferenciação automática. Se os gradientes forem calculados nesse contexto, o cálculo do gradiente também será registrado. Como resultado, a mesma API também funciona para gradientes de ordem superior.

Por exemplo:

x = tf.Variable(1.0)  # Create a Tensorflow variable initialized to 1.0

with tf.GradientTape() as t2:
  with tf.GradientTape() as t1:
    y = x * x * x

  # Compute the gradient inside the outer `t2` context manager
  # which means the gradient computation is differentiable as well.
  dy_dx = t1.gradient(y, x)
d2y_dx2 = t2.gradient(dy_dx, x)

print('dy_dx:', dy_dx.numpy())  # 3 * x**2 => 3.0
print('d2y_dx2:', d2y_dx2.numpy())  # 6 * x => 6.0

dy_dx: 3.0
d2y_dx2: 6.0

Embora isso forneça a segunda derivada de uma função escalar , esse padrão não se generaliza para produzir uma matriz hessiana, pois tf.GradientTape.gradient apenas calcula o gradiente de um escalar. Para construir uma matriz hessiana , vá para o exemplo hessiano na seção jacobiana .

"Chamadas aninhadas para tf.GradientTape.gradient " é um bom padrão quando você está calculando um escalar a partir de um gradiente e, em seguida, o escalar resultante atua como uma fonte para um segundo cálculo de gradiente, como no exemplo a seguir.

Exemplo: regularização de gradiente de entrada

Muitos modelos são suscetíveis a "exemplos adversários". Essa coleção de técnicas modifica a entrada do modelo para confundir a saída do modelo. A implementação mais simples — como o exemplo Adversarial usando o ataque Fast Gradient Signed Method — dá um único passo ao longo do gradiente da saída em relação à entrada; o "gradiente de entrada".

Uma técnica para aumentar a robustez a exemplos adversários é a regularização do gradiente de entrada (Finlay & Oberman, 2019), que tenta minimizar a magnitude do gradiente de entrada. Se o gradiente de entrada for pequeno, a mudança na saída também deve ser pequena.

Abaixo está uma implementação ingênua de regularização de gradiente de entrada. A implementação é:

Calcule o gradiente da saída em relação à entrada usando uma fita interna.
Calcule a magnitude desse gradiente de entrada.
Calcule o gradiente dessa magnitude em relação ao modelo.

x = tf.random.normal([7, 5])

layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)

with tf.GradientTape() as t2:
  # The inner tape only takes the gradient with respect to the input,
  # not the variables.
  with tf.GradientTape(watch_accessed_variables=False) as t1:
    t1.watch(x)
    y = layer(x)
    out = tf.reduce_sum(layer(x)**2)
  # 1. Calculate the input gradient.
  g1 = t1.gradient(out, x)
  # 2. Calculate the magnitude of the input gradient.
  g1_mag = tf.norm(g1)

# 3. Calculate the gradient of the magnitude with respect to the model.
dg1_mag = t2.gradient(g1_mag, layer.trainable_variables)

[var.shape for var in dg1_mag]

[TensorShape([5, 10]), TensorShape([10])]

Jacobianos

Todos os exemplos anteriores pegaram os gradientes de um alvo escalar em relação a alguns tensores de origem.

A matriz Jacobiana representa os gradientes de uma função com valor vetorial. Cada linha contém o gradiente de um dos elementos do vetor.

O método tf.GradientTape.jacobian permite calcular eficientemente uma matriz Jacobiana.

Observe que:

Como gradient : O argumento de sources pode ser um tensor ou um contêiner de tensores.
Ao contrário de gradient : O tensor de target deve ser um único tensor.

Fonte escalar

Como primeiro exemplo, aqui está o Jacobiano de um vetor-alvo em relação a uma fonte escalar.

x = tf.linspace(-10.0, 10.0, 200+1)
delta = tf.Variable(0.0)

with tf.GradientTape() as tape:
  y = tf.nn.sigmoid(x+delta)

dy_dx = tape.jacobian(y, delta)

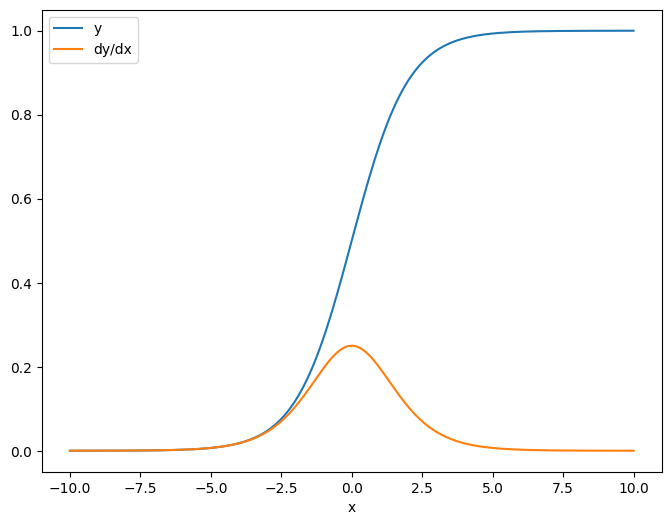
Quando você pega o Jacobiano em relação a um escalar o resultado tem a forma do target , e dá o gradiente de cada elemento em relação à fonte:

print(y.shape)
print(dy_dx.shape)

(201,)
(201,)

plt.plot(x.numpy(), y, label='y')
plt.plot(x.numpy(), dy_dx, label='dy/dx')
plt.legend()
_ = plt.xlabel('x')

png

Fonte do tensor

Quer a entrada seja escalar ou tensor, tf.GradientTape.jacobian calcula eficientemente o gradiente de cada elemento da fonte em relação a cada elemento do(s) destino(s).

Por exemplo, a saída desta camada tem uma forma de (10, 7) :

x = tf.random.normal([7, 5])
layer = tf.keras.layers.Dense(10, activation=tf.nn.relu)

with tf.GradientTape(persistent=True) as tape:
  y = layer(x)

y.shape

TensorShape([7, 10])

E a forma do kernel da camada é (5, 10) :

layer.kernel.shape

TensorShape([5, 10])

A forma do Jacobiano da saída em relação ao kernel são essas duas formas concatenadas:

j = tape.jacobian(y, layer.kernel)
j.shape

TensorShape([7, 10, 5, 10])

Se você somar as dimensões do destino, ficará com o gradiente da soma que teria sido calculada por tf.GradientTape.gradient :

g = tape.gradient(y, layer.kernel)
print('g.shape:', g.shape)

j_sum = tf.reduce_sum(j, axis=[0, 1])
delta = tf.reduce_max(abs(g - j_sum)).numpy()
assert delta < 1e-3
print('delta:', delta)

g.shape: (5, 10)
delta: 2.3841858e-07

Exemplo: Hesse

Embora tf.GradientTape não forneça um método explícito para construir uma matriz Hessiana , é possível construir uma usando o método tf.GradientTape.jacobian .

x = tf.random.normal([7, 5])
layer1 = tf.keras.layers.Dense(8, activation=tf.nn.relu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.relu)

with tf.GradientTape() as t2:
  with tf.GradientTape() as t1:
    x = layer1(x)
    x = layer2(x)
    loss = tf.reduce_mean(x**2)

  g = t1.gradient(loss, layer1.kernel)

h = t2.jacobian(g, layer1.kernel)

print(f'layer.kernel.shape: {layer1.kernel.shape}')
print(f'h.shape: {h.shape}')

layer.kernel.shape: (5, 8)
h.shape: (5, 8, 5, 8)

Para usar este Hessiano para uma etapa do método de Newton , você primeiro achataria seus eixos em uma matriz e achataria o gradiente em um vetor:

n_params = tf.reduce_prod(layer1.kernel.shape)

g_vec = tf.reshape(g, [n_params, 1])
h_mat = tf.reshape(h, [n_params, n_params])

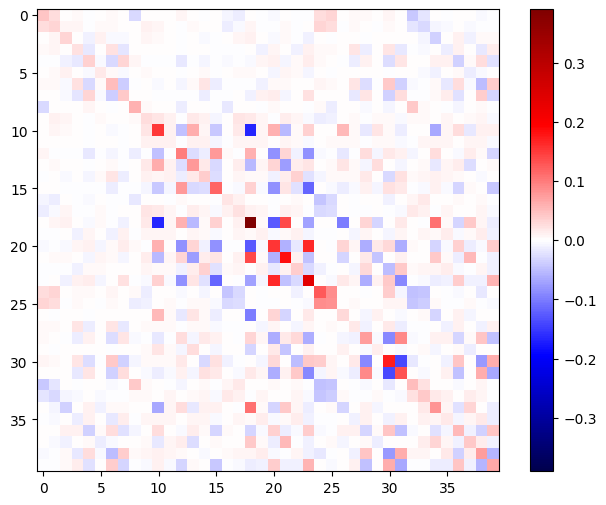
A matriz Hessiana deve ser simétrica:

def imshow_zero_center(image, **kwargs):
  lim = tf.reduce_max(abs(image))
  plt.imshow(image, vmin=-lim, vmax=lim, cmap='seismic', **kwargs)
  plt.colorbar()

imshow_zero_center(h_mat)

png

A etapa de atualização do método de Newton é mostrada abaixo:

eps = 1e-3
eye_eps = tf.eye(h_mat.shape[0])*eps

# X(k+1) = X(k) - (∇²f(X(k)))^-1 @ ∇f(X(k))
# h_mat = ∇²f(X(k))
# g_vec = ∇f(X(k))
update = tf.linalg.solve(h_mat + eye_eps, g_vec)

# Reshape the update and apply it to the variable.
_ = layer1.kernel.assign_sub(tf.reshape(update, layer1.kernel.shape))

Embora isso seja relativamente simples para um único tf.Variable , aplicar isso a um modelo não trivial exigiria uma concatenação cuidadosa e fatiamento para produzir um Hessian completo em várias variáveis.

Lote Jacobiano

Em alguns casos, você deseja obter o Jacobiano de cada uma de uma pilha de destinos em relação a uma pilha de fontes, onde os Jacobianos de cada par de destino-fonte são independentes.

Por exemplo, aqui a entrada x é moldada (batch, ins) e a saída y é moldada (batch, outs) :

x = tf.random.normal([7, 5])

layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)

with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
  tape.watch(x)
  y = layer1(x)
  y = layer2(y)

y.shape

TensorShape([7, 6])

O Jacobiano completo de y em relação a x tem uma forma de (batch, ins, batch, outs) , mesmo se você quiser apenas (batch, ins, outs) :

j = tape.jacobian(y, x)
j.shape

TensorShape([7, 6, 7, 5])

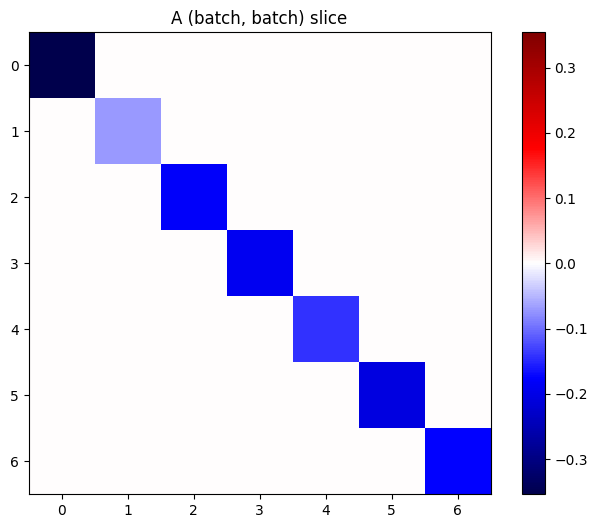
Se os gradientes de cada item na pilha são independentes, então cada fatia (batch, batch) deste tensor é uma matriz diagonal:

imshow_zero_center(j[:, 0, :, 0])
_ = plt.title('A (batch, batch) slice')

png

def plot_as_patches(j):
  # Reorder axes so the diagonals will each form a contiguous patch.
  j = tf.transpose(j, [1, 0, 3, 2])
  # Pad in between each patch.
  lim = tf.reduce_max(abs(j))
  j = tf.pad(j, [[0, 0], [1, 1], [0, 0], [1, 1]],
             constant_values=-lim)
  # Reshape to form a single image.
  s = j.shape
  j = tf.reshape(j, [s[0]*s[1], s[2]*s[3]])
  imshow_zero_center(j, extent=[-0.5, s[2]-0.5, s[0]-0.5, -0.5])

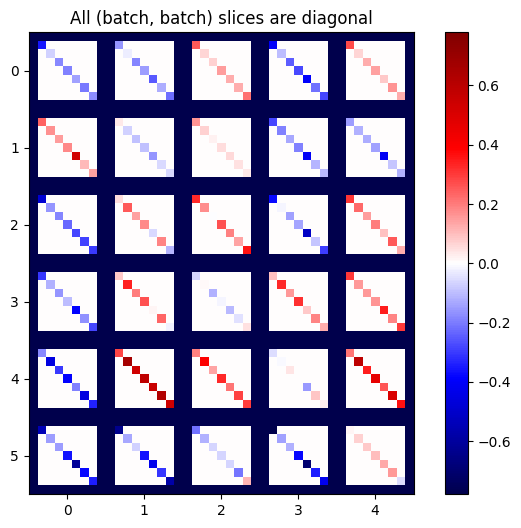
plot_as_patches(j)
_ = plt.title('All (batch, batch) slices are diagonal')

png

Para obter o resultado desejado, você pode somar a dimensão do batch duplicado ou selecionar as diagonais usando tf.einsum :

j_sum = tf.reduce_sum(j, axis=2)
print(j_sum.shape)
j_select = tf.einsum('bxby->bxy', j)
print(j_select.shape)

(7, 6, 5)
(7, 6, 5)

Seria muito mais eficiente fazer o cálculo sem a dimensão extra em primeiro lugar. O método tf.GradientTape.batch_jacobian faz exatamente isso:

jb = tape.batch_jacobian(y, x)
jb.shape

WARNING:tensorflow:5 out of the last 5 calls to <function pfor.<locals>.f at 0x7f7d601250e0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for  more details.
TensorShape([7, 6, 5])

error = tf.reduce_max(abs(jb - j_sum))
assert error < 1e-3
print(error.numpy())

0.0

x = tf.random.normal([7, 5])

layer1 = tf.keras.layers.Dense(8, activation=tf.nn.elu)
bn = tf.keras.layers.BatchNormalization()
layer2 = tf.keras.layers.Dense(6, activation=tf.nn.elu)

with tf.GradientTape(persistent=True, watch_accessed_variables=False) as tape:
  tape.watch(x)
  y = layer1(x)
  y = bn(y, training=True)
  y = layer2(y)

j = tape.jacobian(y, x)
print(f'j.shape: {j.shape}')

WARNING:tensorflow:6 out of the last 6 calls to <function pfor.<locals>.f at 0x7f7cf062fa70> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for  more details.
j.shape: (7, 6, 7, 5)

plot_as_patches(j)

_ = plt.title('These slices are not diagonal')
_ = plt.xlabel("Don't use `batch_jacobian`")

png

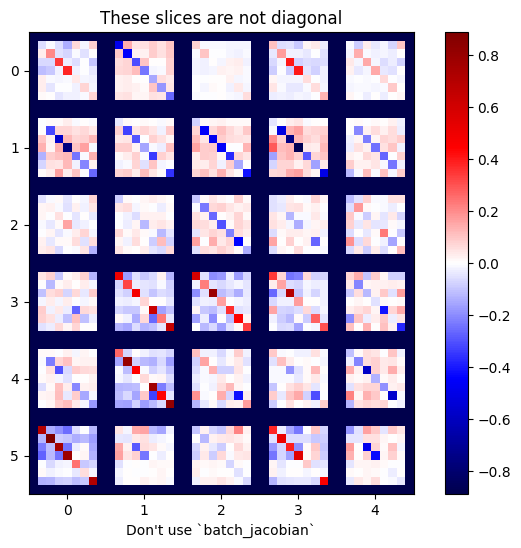
Nesse caso, batch_jacobian ainda é executado e retorna algo com a forma esperada, mas seu conteúdo tem um significado pouco claro:

jb = tape.batch_jacobian(y, x)
print(f'jb.shape: {jb.shape}')

jb.shape: (7, 6, 5)