 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Ce tutoriel explore l' apprentissage fédéré en partie local, où certains paramètres du client ne sont jamais agrégés sur le serveur. Ceci est utile pour les modèles avec des paramètres spécifiques à l'utilisateur (par exemple, les modèles de factorisation matricielle) et pour la formation dans les paramètres de communication limités. Nous misons sur des concepts introduits dans l' apprentissage fédéré pour l' image de classification tutoriel; comme dans ce tutoriel, nous présentons des API de haut niveau dans tff.learning pour la formation et l' évaluation fédérée.
Nous commençons par motiver l' apprentissage fédérée partiellement locale pour factorisation de la matrice . Nous décrivons Federated la reconstruction , un algorithme pratique pour l' apprentissage fédéré en partie à l' échelle locale. Nous préparons l'ensemble de données MovieLens 1M, construisons un modèle partiellement local, l'entraînons et l'évaluons.
!pip install --quiet --upgrade tensorflow-federated-nightly
!pip install --quiet --upgrade nest-asyncio
import nest_asyncio
nest_asyncio.apply()
import collections
import functools
import io
import os
import requests
import zipfile
from typing import List, Optional, Tuple
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow as tf
import tensorflow_federated as tff
np.random.seed(42)
Contexte : factorisation matricielle
Matrice factorisation a été une technique historiquement populaire pour les recommandations d' apprentissage et l' intégration des représentations des éléments basés sur les interactions des utilisateurs. L'exemple canonique est la recommandation de film, où il y a \(n\) utilisateurs et \(m\) films, et les utilisateurs ont noté des films. Pour un utilisateur donné, nous utilisons son historique de classement et les classements d'utilisateurs similaires pour prédire les classements de l'utilisateur pour les films qu'il n'a pas vus. Si nous avons un modèle qui peut prédire les notes, il est facile de recommander aux utilisateurs de nouveaux films qu'ils apprécieront.
Pour cette tâche, il est utile de représenter les évaluations des utilisateurs comme \(n \times m\) matrice \(R\):

Cette matrice est généralement clairsemée, car les utilisateurs ne voient généralement qu'une petite fraction des films dans l'ensemble de données. La sortie de la factorisation de la matrice est de deux matrices: une \(n \times k\) matrice \(U\) représentant \(k\)embeddings utilisateur de dimension pour chaque utilisateur, et un \(m \times k\) matrice \(I\) représentant \(k\)embeddings d'éléments de dimension pour chaque élément. L'objectif de la formation plus simple est de faire en sorte que le produit scalaire de plongements utilisateur et poste sont prédictifs des évaluations observées \(O\):
\[argmin_{U,I} \sum_{(u, i) \in O} (R_{ui} - U_u I_i^T)^2\]
Cela équivaut à minimiser l'erreur quadratique moyenne entre les notes observées et les notes prédites en prenant le produit scalaire de l'utilisateur et des plongements d'élément correspondants. Une autre façon d'interpréter ceci est que cela assure que \(R \approx UI^T\) pour les cotes connues, d' où « matrice factorisation ». Si cela prête à confusion, ne vous inquiétez pas, nous n'aurons pas besoin de connaître les détails de la factorisation matricielle pour le reste du didacticiel.
Exploration des données MovieLens
Commençons par le chargement des MovieLens 1M données, qui se compose de 1,000,209 classement des films de 6040 utilisateurs sur 3706 films.
def download_movielens_data(dataset_path):
"""Downloads and copies MovieLens data to local /tmp directory."""
if dataset_path.startswith('http'):
r = requests.get(dataset_path)
z = zipfile.ZipFile(io.BytesIO(r.content))
z.extractall(path='/tmp')
else:
tf.io.gfile.makedirs('/tmp/ml-1m/')
for filename in ['ratings.dat', 'movies.dat', 'users.dat']:
tf.io.gfile.copy(
os.path.join(dataset_path, filename),
os.path.join('/tmp/ml-1m/', filename),
overwrite=True)
download_movielens_data('http://files.grouplens.org/datasets/movielens/ml-1m.zip')
def load_movielens_data(
data_directory: str = "/tmp",
) -> Tuple[pd.DataFrame, pd.DataFrame]:
"""Loads pandas DataFrames for ratings, movies, users from data directory."""
# Load pandas DataFrames from data directory. Assuming data is formatted as
# specified in http://files.grouplens.org/datasets/movielens/ml-1m-README.txt.
ratings_df = pd.read_csv(
os.path.join(data_directory, "ml-1m", "ratings.dat"),
sep="::",
names=["UserID", "MovieID", "Rating", "Timestamp"], engine="python")
movies_df = pd.read_csv(
os.path.join(data_directory, "ml-1m", "movies.dat"),
sep="::",
names=["MovieID", "Title", "Genres"], engine="python")
# Create dictionaries mapping from old IDs to new (remapped) IDs for both
# MovieID and UserID. Use the movies and users present in ratings_df to
# determine the mapping, since movies and users without ratings are unneeded.
movie_mapping = {
old_movie: new_movie for new_movie, old_movie in enumerate(
ratings_df.MovieID.astype("category").cat.categories)
}
user_mapping = {
old_user: new_user for new_user, old_user in enumerate(
ratings_df.UserID.astype("category").cat.categories)
}
# Map each DataFrame consistently using the now-fixed mapping.
ratings_df.MovieID = ratings_df.MovieID.map(movie_mapping)
ratings_df.UserID = ratings_df.UserID.map(user_mapping)
movies_df.MovieID = movies_df.MovieID.map(movie_mapping)
# Remove nulls resulting from some movies being in movies_df but not
# ratings_df.
movies_df = movies_df[pd.notnull(movies_df.MovieID)]
return ratings_df, movies_df
Chargeons et explorons quelques Pandas DataFrames contenant la notation et les données du film.
ratings_df, movies_df = load_movielens_data()
Nous pouvons voir que chaque exemple de notation a une notation de 1 à 5, un UserID correspondant, un MovieID correspondant et un horodatage.
ratings_df.head()
Chaque film a un titre et potentiellement plusieurs genres.
movies_df.head()
C'est toujours une bonne idée de comprendre les statistiques de base de l'ensemble de données :
print('Num users:', len(set(ratings_df.UserID)))
print('Num movies:', len(set(ratings_df.MovieID)))
Num users: 6040 Num movies: 3706
ratings = ratings_df.Rating.tolist()
plt.hist(ratings, bins=5)
plt.xticks([1, 2, 3, 4, 5])
plt.ylabel('Count')
plt.xlabel('Rating')
plt.show()
print('Average rating:', np.mean(ratings))
print('Median rating:', np.median(ratings))
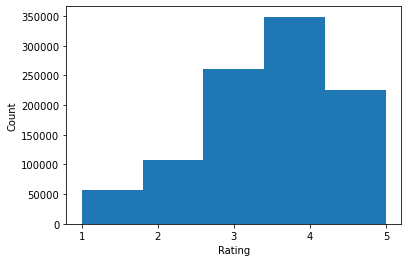
Average rating: 3.581564453029317 Median rating: 4.0
Nous pouvons également tracer les genres de films les plus populaires.
movie_genres_list = movies_df.Genres.tolist()
# Count the number of times each genre describes a movie.
genre_count = collections.defaultdict(int)
for genres in movie_genres_list:
curr_genres_list = genres.split('|')
for genre in curr_genres_list:
genre_count[genre] += 1
genre_name_list, genre_count_list = zip(*genre_count.items())
plt.figure(figsize=(11, 11))
plt.pie(genre_count_list, labels=genre_name_list)
plt.title('MovieLens Movie Genres')
plt.show()
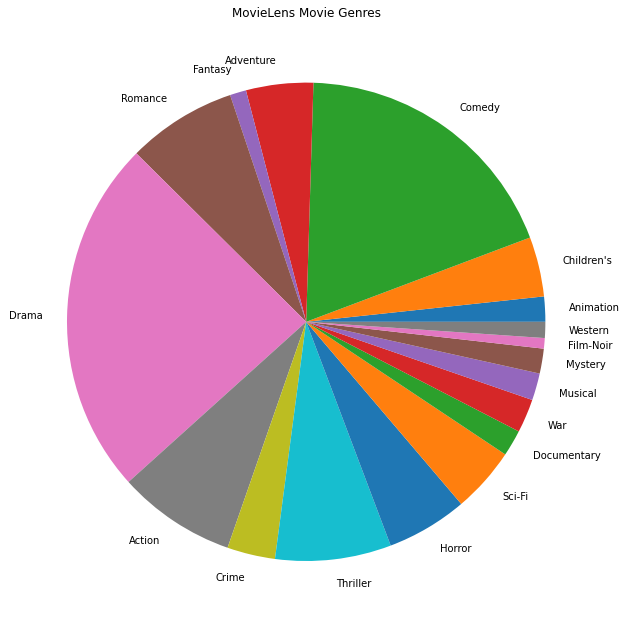
Ces données sont naturellement partitionnées en notes de différents utilisateurs, nous nous attendons donc à une certaine hétérogénéité des données entre les clients. Ci-dessous, nous affichons les genres de films les plus couramment notés pour différents utilisateurs. Nous pouvons observer des différences significatives entre les utilisateurs.
def print_top_genres_for_user(ratings_df, movies_df, user_id):
"""Prints top movie genres for user with ID user_id."""
user_ratings_df = ratings_df[ratings_df.UserID == user_id]
movie_ids = user_ratings_df.MovieID
genre_count = collections.Counter()
for movie_id in movie_ids:
genres_string = movies_df[movies_df.MovieID == movie_id].Genres.tolist()[0]
for genre in genres_string.split('|'):
genre_count[genre] += 1
print(f'\nFor user {user_id}:')
for (genre, freq) in genre_count.most_common(5):
print(f'{genre} was rated {freq} times')
print_top_genres_for_user(ratings_df, movies_df, user_id=0)
print_top_genres_for_user(ratings_df, movies_df, user_id=10)
print_top_genres_for_user(ratings_df, movies_df, user_id=19)
For user 0: Drama was rated 21 times Children's was rated 20 times Animation was rated 18 times Musical was rated 14 times Comedy was rated 14 times For user 10: Comedy was rated 84 times Drama was rated 54 times Romance was rated 22 times Thriller was rated 18 times Action was rated 9 times For user 19: Action was rated 17 times Sci-Fi was rated 9 times Thriller was rated 9 times Drama was rated 6 times Crime was rated 5 times
Prétraitement des données MovieLens
Nous préparons maintenant l'ensemble de données MovieLens comme une liste de tf.data.Dataset s représentant les données de chaque utilisateur pour une utilisation avec TFF.
Nous implémentons deux fonctions :
-
create_tf_datasets: prend nos notes dataframe et produit une liste des utilisateurs-splittf.data.Datasets. -
split_tf_datasets: prend une liste de jeux de données et les divise en train / val / test par l' utilisateur, de sorte que les ensembles de val / test ne contiennent que des évaluations des utilisateurs invisibles pendant la formation. En règle générale dans la matrice centralisée norme factorisation nous diviser en fait pour que les val / ensembles de test contiennent évaluations détenus à des utilisateurs vus, puisque les utilisateurs invisibles ne sont pas incorporations utilisateur. Dans notre cas, nous verrons plus tard que l'approche que nous utilisons pour activer la factorisation matricielle en FL permet également de reconstruire rapidement les plongements utilisateur pour les utilisateurs invisibles.
def create_tf_datasets(ratings_df: pd.DataFrame,
batch_size: int = 1,
max_examples_per_user: Optional[int] = None,
max_clients: Optional[int] = None) -> List[tf.data.Dataset]:
"""Creates TF Datasets containing the movies and ratings for all users."""
num_users = len(set(ratings_df.UserID))
# Optionally limit to `max_clients` to speed up data loading.
if max_clients is not None:
num_users = min(num_users, max_clients)
def rating_batch_map_fn(rating_batch):
"""Maps a rating batch to an OrderedDict with tensor values."""
# Each example looks like: {x: movie_id, y: rating}.
# We won't need the UserID since each client will only look at their own
# data.
return collections.OrderedDict([
("x", tf.cast(rating_batch[:, 1:2], tf.int64)),
("y", tf.cast(rating_batch[:, 2:3], tf.float32))
])
tf_datasets = []
for user_id in range(num_users):
# Get subset of ratings_df belonging to a particular user.
user_ratings_df = ratings_df[ratings_df.UserID == user_id]
tf_dataset = tf.data.Dataset.from_tensor_slices(user_ratings_df)
# Define preprocessing operations.
tf_dataset = tf_dataset.take(max_examples_per_user).shuffle(
buffer_size=max_examples_per_user, seed=42).batch(batch_size).map(
rating_batch_map_fn,
num_parallel_calls=tf.data.experimental.AUTOTUNE)
tf_datasets.append(tf_dataset)
return tf_datasets
def split_tf_datasets(
tf_datasets: List[tf.data.Dataset],
train_fraction: float = 0.8,
val_fraction: float = 0.1,
) -> Tuple[List[tf.data.Dataset], List[tf.data.Dataset], List[tf.data.Dataset]]:
"""Splits a list of user TF datasets into train/val/test by user.
"""
np.random.seed(42)
np.random.shuffle(tf_datasets)
train_idx = int(len(tf_datasets) * train_fraction)
val_idx = int(len(tf_datasets) * (train_fraction + val_fraction))
# Note that the val and test data contains completely different users, not
# just unseen ratings from train users.
return (tf_datasets[:train_idx], tf_datasets[train_idx:val_idx],
tf_datasets[val_idx:])
# We limit the number of clients to speed up dataset creation. Feel free to pass
# max_clients=None to load all clients' data.
tf_datasets = create_tf_datasets(
ratings_df=ratings_df,
batch_size=5,
max_examples_per_user=300,
max_clients=2000)
# Split the ratings into training/val/test by client.
tf_train_datasets, tf_val_datasets, tf_test_datasets = split_tf_datasets(
tf_datasets,
train_fraction=0.8,
val_fraction=0.1)
Comme vérification rapide, nous pouvons imprimer un lot de données d'entraînement. Nous pouvons voir que chaque exemple individuel contient un MovieID sous la touche "x" et une note sous la touche "y". Notez que nous n'aurons pas besoin de l'ID utilisateur puisque chaque utilisateur ne voit que ses propres données.
print(next(iter(tf_train_datasets[0])))
OrderedDict([('x', <tf.Tensor: shape=(5, 1), dtype=int64, numpy=
array([[1907],
[2891],
[1574],
[2785],
[2775]])>), ('y', <tf.Tensor: shape=(5, 1), dtype=float32, numpy=
array([[3.],
[3.],
[3.],
[4.],
[3.]], dtype=float32)>)])
Nous pouvons tracer un histogramme indiquant le nombre d'évaluations par utilisateur.
def count_examples(curr_count, batch):
return curr_count + tf.size(batch['x'])
num_examples_list = []
# Compute number of examples for every other user.
for i in range(0, len(tf_train_datasets), 2):
num_examples = tf_train_datasets[i].reduce(tf.constant(0), count_examples).numpy()
num_examples_list.append(num_examples)
plt.hist(num_examples_list, bins=10)
plt.ylabel('Count')
plt.xlabel('Number of Examples')
plt.show()
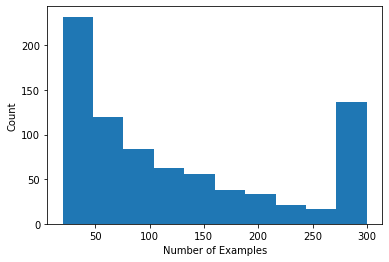
Maintenant que nous avons chargé et exploré les données, nous allons discuter de la manière d'intégrer la factorisation matricielle à l'apprentissage fédéré. En cours de route, nous motiverons un apprentissage fédéré partiellement local.
Apporter la factorisation matricielle à FL
Alors que la factorisation matricielle a été traditionnellement utilisée dans les paramètres centralisés, elle est particulièrement pertinente dans l'apprentissage fédéré : les évaluations des utilisateurs peuvent résider sur des appareils clients distincts, et nous pouvons vouloir apprendre les intégrations et les recommandations pour les utilisateurs et les éléments sans centraliser les données. Étant donné que chaque utilisateur a une intégration utilisateur correspondante, il est naturel que chaque client stocke son intégration utilisateur - cela évolue beaucoup mieux qu'un serveur central stockant toutes les intégrations utilisateur.
Une proposition pour amener la factorisation matricielle à FL est la suivante :
- Le serveur stocke et envoie la matrice de l' élément \(I\) aux clients de l' échantillon chaque tour
- Les clients mettent à jour la matrice de l' élément et leur utilisateur personnel intégrant \(U_u\) utilisant SGD l'objectif ci - dessus
- Les mises à jour \(I\) sont agrégés sur le serveur, la mise à jour la copie du serveur de \(I\) pour le prochain tour
Cette approche est en partie locale , c'est - , certains paramètres du client ne sont jamais agrégés par le serveur. Bien que cette approche soit attrayante, elle exige des clients qu'ils maintiennent l'état d'un cycle à l'autre, à savoir leurs intégrations d'utilisateurs. Les algorithmes fédérés avec état sont moins appropriés pour les paramètres FL inter-appareils : dans ces paramètres, la taille de la population est souvent bien supérieure au nombre de clients qui participent à chaque cycle, et un client participe généralement au plus une fois au cours du processus de formation. En plus de compter sur l' état qui ne peut pas être initialisé, les algorithmes stateful peuvent entraîner une dégradation des performances dans un contexte multi-appareil en raison de l' état se rassis lorsque les clients sont rarement échantillonnés. Il est important de noter que dans le cadre de la factorisation matricielle, un algorithme avec état conduit à ce que tous les clients invisibles manquent d'intégrations d'utilisateurs formés, et dans une formation à grande échelle, la majorité des utilisateurs peuvent être invisibles. Pour en savoir plus sur la motivation des algorithmes sans état dans FL multi-appareils, voir Wang et al. 2021 Sec. 3.1.1 et Reddi et al. 2020 Sec. 5.1 .
Reconstruction fédéré ( Singhal et al. 2021 ) est une alternative à l'approche sans état mentionné ci - dessus. L'idée clé est qu'au lieu de stocker les intégrations d'utilisateurs d'un cycle à l'autre, les clients reconstruisent les intégrations d'utilisateurs en cas de besoin. Lorsque FedRecon est appliqué à la factorisation matricielle, la formation se déroule comme suit :
- Le serveur stocke et envoie la matrice de l' élément \(I\) aux clients de l' échantillon chaque tour
- Chaque client se fige \(I\) et forme leur enrobage utilisateur \(U_u\) en utilisant une ou plusieurs étapes de SGD (reconstruction)
- Chaque client se fige \(U_u\) et trains \(I\) en utilisant une ou plusieurs étapes de SGD
- Les mises à jour \(I\) sont agrégées entre les utilisateurs, la mise à jour la copie du serveur de \(I\) pour le prochain tour
Cette approche n'exige pas que les clients maintiennent l'état d'un cycle à l'autre. Les auteurs montrent également dans l'article que cette méthode conduit à une reconstruction rapide des intégrations d'utilisateurs pour les clients invisibles (Sec. 4.2, Fig. 3 et Tableau 1), permettant à la majorité des clients qui ne participent pas à la formation d'avoir un modèle formé. , permettant des recommandations pour ces clients.
Définir le modèle
Nous définirons ensuite le modèle de factorisation matricielle locale à entraîner sur les appareils clients. Ce modèle comprendra la matrice de l' article complet \(I\) et un seul utilisateur plongement \(U_u\) pour le client \(u\). Notez que les clients auront pas besoin de stocker la matrice utilisateur complète \(U\).
Nous allons définir les éléments suivants :
-
UserEmbedding: simple couche Keras représentant un seulnum_latent_factorsplongement utilisateur -dimensionnelle. -
get_matrix_factorization_model: une fonction qui renvoie untff.learning.reconstruction.Modelcontenant la logique de modèle, y compris des couches qui sont globalement regroupées sur le serveur et qui restent couches local. Nous avons besoin de ces informations supplémentaires pour initialiser le processus de formation de la reconstruction fédérée. Ici , nous produisons letff.learning.reconstruction.Modeld'un modèle à l' aide Kerastff.learning.reconstruction.from_keras_model. Semblable àtff.learning.Model, nous pouvons également mettre en œuvre une mesuretff.learning.reconstruction.Modelen mettant en œuvre l'interface de classe.
class UserEmbedding(tf.keras.layers.Layer):
"""Keras layer representing an embedding for a single user, used below."""
def __init__(self, num_latent_factors, **kwargs):
super().__init__(**kwargs)
self.num_latent_factors = num_latent_factors
def build(self, input_shape):
self.embedding = self.add_weight(
shape=(1, self.num_latent_factors),
initializer='uniform',
dtype=tf.float32,
name='UserEmbeddingKernel')
super().build(input_shape)
def call(self, inputs):
return self.embedding
def compute_output_shape(self):
return (1, self.num_latent_factors)
def get_matrix_factorization_model(
num_items: int,
num_latent_factors: int) -> tff.learning.reconstruction.Model:
"""Defines a Keras matrix factorization model."""
# Layers with variables will be partitioned into global and local layers.
# We'll pass this to `tff.learning.reconstruction.from_keras_model`.
global_layers = []
local_layers = []
# Extract the item embedding.
item_input = tf.keras.layers.Input(shape=[1], name='Item')
item_embedding_layer = tf.keras.layers.Embedding(
num_items,
num_latent_factors,
name='ItemEmbedding')
global_layers.append(item_embedding_layer)
flat_item_vec = tf.keras.layers.Flatten(name='FlattenItems')(
item_embedding_layer(item_input))
# Extract the user embedding.
user_embedding_layer = UserEmbedding(
num_latent_factors,
name='UserEmbedding')
local_layers.append(user_embedding_layer)
# The item_input never gets used by the user embedding layer,
# but this allows the model to directly use the user embedding.
flat_user_vec = user_embedding_layer(item_input)
# Compute the dot product between the user embedding, and the item one.
pred = tf.keras.layers.Dot(
1, normalize=False, name='Dot')([flat_user_vec, flat_item_vec])
input_spec = collections.OrderedDict(
x=tf.TensorSpec(shape=[None, 1], dtype=tf.int64),
y=tf.TensorSpec(shape=[None, 1], dtype=tf.float32))
model = tf.keras.Model(inputs=item_input, outputs=pred)
return tff.learning.reconstruction.from_keras_model(
keras_model=model,
global_layers=global_layers,
local_layers=local_layers,
input_spec=input_spec)
À l'interface analogue pour calculer la moyenne fédérée, l'interface pour la reconstruction fédérée attend un model_fn sans argument qui renvoie une tff.learning.reconstruction.Model .
# This will be used to produce our training process.
# User and item embeddings will be 50-dimensional.
model_fn = functools.partial(
get_matrix_factorization_model,
num_items=3706,
num_latent_factors=50)
Nous allons ensuite définir loss_fn et metrics_fn , où loss_fn est une fonction sans argument retourner une perte Keras à utiliser pour former le modèle et metrics_fn est une fonction sans argument retourner une liste de mesures KERAS pour l' évaluation. Ceux-ci sont nécessaires pour construire les calculs d'entraînement et d'évaluation.
Nous utiliserons l'erreur quadratique moyenne comme perte, comme mentionné ci-dessus. Pour l'évaluation, nous utiliserons la précision de l'évaluation (lorsque le produit scalaire prévu du modèle est arrondi au nombre entier le plus proche, à quelle fréquence correspond-il à l'évaluation de l'étiquette ?).
class RatingAccuracy(tf.keras.metrics.Mean):
"""Keras metric computing accuracy of reconstructed ratings."""
def __init__(self,
name: str = 'rating_accuracy',
**kwargs):
super().__init__(name=name, **kwargs)
def update_state(self,
y_true: tf.Tensor,
y_pred: tf.Tensor,
sample_weight: Optional[tf.Tensor] = None):
absolute_diffs = tf.abs(y_true - y_pred)
# A [batch_size, 1] tf.bool tensor indicating correctness within the
# threshold for each example in a batch. A 0.5 threshold corresponds
# to correctness when predictions are rounded to the nearest whole
# number.
example_accuracies = tf.less_equal(absolute_diffs, 0.5)
super().update_state(example_accuracies, sample_weight=sample_weight)
loss_fn = lambda: tf.keras.losses.MeanSquaredError()
metrics_fn = lambda: [RatingAccuracy()]
Formation et évaluation
Maintenant, nous avons tout ce dont nous avons besoin pour définir le processus de formation. Une différence importante de l' interface pour la reconstruction_optimizer_fn moyenne fédérée est que nous passons maintenant dans un reconstruction_optimizer_fn , qui sera utilisé lors de la reconstruction des paramètres locaux (dans notre cas, incorporations utilisateur). Il est généralement raisonnable d'utiliser SGD ici, avec un similaire ou légèrement plus bas taux d' apprentissage que le taux d' apprentissage client optimiseur. Nous fournissons une configuration de travail ci-dessous. Cela n'a pas été soigneusement réglé, alors n'hésitez pas à jouer avec différentes valeurs.
Consultez la documentation pour plus de détails et d' options.
# We'll use this by doing:
# state = training_process.initialize()
# state, metrics = training_process.next(state, federated_train_data)
training_process = tff.learning.reconstruction.build_training_process(
model_fn=model_fn,
loss_fn=loss_fn,
metrics_fn=metrics_fn,
server_optimizer_fn=lambda: tf.keras.optimizers.SGD(1.0),
client_optimizer_fn=lambda: tf.keras.optimizers.SGD(0.5),
reconstruction_optimizer_fn=lambda: tf.keras.optimizers.SGD(0.1))
Nous pouvons également définir un calcul pour évaluer notre modèle global formé.
# We'll use this by doing:
# eval_metrics = evaluation_computation(state.model, tf_val_datasets)
# where `state` is the state from the training process above.
evaluation_computation = tff.learning.reconstruction.build_federated_evaluation(
model_fn,
loss_fn=loss_fn,
metrics_fn=metrics_fn,
reconstruction_optimizer_fn=functools.partial(
tf.keras.optimizers.SGD, 0.1))
Nous pouvons initialiser l'état du processus d'apprentissage et l'examiner. Plus important encore, nous pouvons voir que cet état de serveur ne stocke que les variables d'élément (actuellement initialisées de manière aléatoire) et non les intégrations d'utilisateurs.
state = training_process.initialize()
print(state.model)
print('Item variables shape:', state.model.trainable[0].shape)
ModelWeights(trainable=[array([[-0.02840446, 0.01196523, -0.01864688, ..., 0.03020107,
0.00121176, 0.00146852],
[ 0.01330637, 0.04741272, -0.01487445, ..., -0.03352419,
0.0104811 , 0.03506917],
[-0.04132779, 0.04883525, -0.04799002, ..., 0.00246904,
0.00586842, 0.01506213],
...,
[ 0.0216659 , 0.00734354, 0.00471039, ..., 0.01596491,
-0.00220431, -0.01559857],
[-0.00319657, -0.01740328, 0.02808609, ..., -0.00501985,
-0.03850871, -0.03844522],
[ 0.03791947, -0.00035037, 0.04217024, ..., 0.00365371,
0.00283421, 0.00897921]], dtype=float32)], non_trainable=[])
Item variables shape: (3706, 50)
Nous pouvons également essayer d'évaluer notre modèle initialisé de manière aléatoire sur des clients de validation. L'évaluation de la reconstruction fédérée implique ici les éléments suivants :
- Le serveur envoie la matrice de l' article \(I\) aux clients de l' évaluation de l' échantillon
- Chaque client se fige \(I\) et forme leur enrobage utilisateur \(U_u\) en utilisant une ou plusieurs étapes de SGD (reconstruction)
- Chaque client calcule la perte et les paramètres en utilisant le serveur \(I\) et reconstruit \(U_u\) sur une partie invisible de leurs données locales
- Les pertes et les mesures sont moyennées entre les utilisateurs pour calculer les pertes et les mesures globales
Notez que les étapes 1 et 2 sont les mêmes que pour la formation. Cette connexion est importante, car la formation de la même façon que nous évaluons conduit à une forme de méta-apprentissage, ou d' apprendre à apprendre. Dans ce cas, le modèle apprend à apprendre des variables globales (matrice d'éléments) qui conduisent à une reconstruction performante des variables locales (intégrations utilisateur). Pour en savoir plus, voir Sec. 4.2 du papier.
Il est également important que les étapes 2 et 3 soient effectuées en utilisant des portions disjointes des données locales des clients, afin d'assurer une évaluation juste. Par défaut, le processus d'apprentissage et le calcul d'évaluation utilisent tous les deux un exemple sur deux pour la reconstruction et utilisent l'autre moitié après la reconstruction. Ce comportement peut être personnalisé à l' aide du dataset_split_fn argument (nous allons explorer cette plus tard).
# We shouldn't expect good evaluation results here, since we haven't trained
# yet!
eval_metrics = evaluation_computation(state.model, tf_val_datasets)
print('Initial Eval:', eval_metrics['eval'])
Initial Eval: OrderedDict([('loss', 14.340279), ('rating_accuracy', 0.0)])
Nous pouvons ensuite essayer d'exécuter une série d'entraînements. Pour rendre les choses plus réalistes, nous échantillonnerons 50 clients par tour au hasard sans remplacement. Nous devrions toujours nous attendre à ce que les métriques d'entraînement soient médiocres, car nous ne faisons qu'une seule série d'entraînement.
federated_train_data = np.random.choice(tf_train_datasets, size=50, replace=False).tolist()
state, metrics = training_process.next(state, federated_train_data)
print(f'Train metrics:', metrics['train'])
Train metrics: OrderedDict([('rating_accuracy', 0.0), ('loss', 14.317455)])
Mettons maintenant en place une boucle d'entraînement pour s'entraîner sur plusieurs tours.
NUM_ROUNDS = 20
train_losses = []
train_accs = []
state = training_process.initialize()
# This may take a couple minutes to run.
for i in range(NUM_ROUNDS):
federated_train_data = np.random.choice(tf_train_datasets, size=50, replace=False).tolist()
state, metrics = training_process.next(state, federated_train_data)
print(f'Train round {i}:', metrics['train'])
train_losses.append(metrics['train']['loss'])
train_accs.append(metrics['train']['rating_accuracy'])
eval_metrics = evaluation_computation(state.model, tf_val_datasets)
print('Final Eval:', eval_metrics['eval'])
Train round 0: OrderedDict([('rating_accuracy', 0.0), ('loss', 14.7013445)])
Train round 1: OrderedDict([('rating_accuracy', 0.0), ('loss', 14.459233)])
Train round 2: OrderedDict([('rating_accuracy', 0.0), ('loss', 14.52466)])
Train round 3: OrderedDict([('rating_accuracy', 0.0), ('loss', 14.087793)])
Train round 4: OrderedDict([('rating_accuracy', 0.011243612), ('loss', 11.110232)])
Train round 5: OrderedDict([('rating_accuracy', 0.06366048), ('loss', 8.267054)])
Train round 6: OrderedDict([('rating_accuracy', 0.12331288), ('loss', 5.2693872)])
Train round 7: OrderedDict([('rating_accuracy', 0.14264487), ('loss', 5.1511016)])
Train round 8: OrderedDict([('rating_accuracy', 0.21046545), ('loss', 3.8246362)])
Train round 9: OrderedDict([('rating_accuracy', 0.21320973), ('loss', 3.303812)])
Train round 10: OrderedDict([('rating_accuracy', 0.21651311), ('loss', 3.4864292)])
Train round 11: OrderedDict([('rating_accuracy', 0.23476052), ('loss', 3.0105433)])
Train round 12: OrderedDict([('rating_accuracy', 0.21981856), ('loss', 3.1807854)])
Train round 13: OrderedDict([('rating_accuracy', 0.27683082), ('loss', 2.3382564)])
Train round 14: OrderedDict([('rating_accuracy', 0.26080742), ('loss', 2.7009728)])
Train round 15: OrderedDict([('rating_accuracy', 0.2733109), ('loss', 2.2993557)])
Train round 16: OrderedDict([('rating_accuracy', 0.29282996), ('loss', 2.5278995)])
Train round 17: OrderedDict([('rating_accuracy', 0.30204678), ('loss', 2.060092)])
Train round 18: OrderedDict([('rating_accuracy', 0.2940266), ('loss', 2.0976772)])
Train round 19: OrderedDict([('rating_accuracy', 0.3086304), ('loss', 2.0626144)])
Final Eval: OrderedDict([('loss', 1.9961331), ('rating_accuracy', 0.30322924)])
Nous pouvons tracer la perte d'entraînement et la précision au fil des tours. Les hyperparamètres de ce bloc-notes n'ont pas été soigneusement réglés, alors n'hésitez pas à essayer différents clients par tour, les taux d'apprentissage, le nombre de tours et le nombre total de clients pour améliorer ces résultats.
plt.plot(range(NUM_ROUNDS), train_losses)
plt.ylabel('Train Loss')
plt.xlabel('Round')
plt.title('Train Loss')
plt.show()
plt.plot(range(NUM_ROUNDS), train_accs)
plt.ylabel('Train Accuracy')
plt.xlabel('Round')
plt.title('Train Accuracy')
plt.show()
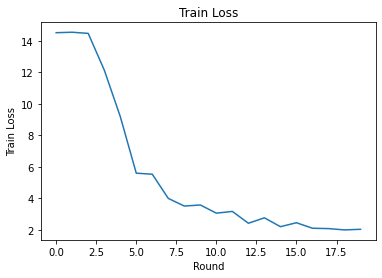
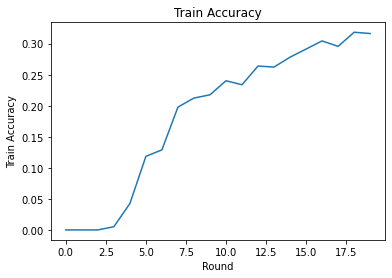
Enfin, nous pouvons calculer des métriques sur un ensemble de test invisible lorsque nous avons terminé le réglage.
eval_metrics = evaluation_computation(state.model, tf_test_datasets)
print('Final Test:', eval_metrics['eval'])
Final Test: OrderedDict([('loss', 1.9566978), ('rating_accuracy', 0.30792442)])
Explorations supplémentaires
Beau travail de réalisation de ce cahier. Nous suggérons les exercices suivants pour explorer davantage l'apprentissage fédéré partiellement local, grossièrement classés par difficulté croissante :
Les implémentations typiques de la moyenne fédérée prennent plusieurs passes locales (époques) sur les données (en plus de prendre une passe sur les données sur plusieurs lots). Pour la reconstruction fédérée, nous pouvons vouloir contrôler le nombre d'étapes séparément pour la reconstruction et la formation post-reconstruction. En passant le
dataset_split_fnargument pour les constructeurs de calcul formation et d' évaluation permet de contrôler le nombre d'étapes et des époques plus deux ensembles de données de reconstruction et de post-reconstruction. À titre d'exercice, essayez d'effectuer 3 périodes locales d'entraînement à la reconstruction, limitées à 50 étapes et 1 période locale d'entraînement post-reconstruction, limitée à 50 étapes. Astuce: vous trouvereztff.learning.reconstruction.build_dataset_split_fnutile. Une fois que vous avez terminé, essayez de régler ces hyperparamètres et d'autres paramètres connexes tels que les taux d'apprentissage et la taille des lots pour obtenir de meilleurs résultats.Le comportement par défaut de la formation et de l'évaluation de Federated Reconstruction consiste à diviser les données locales des clients en deux pour chacune de la reconstruction et de la post-reconstruction. Dans les cas où les clients ont très peu de données locales, il peut être raisonnable de réutiliser les données pour la reconstruction et la post-reconstruction uniquement pour le processus de formation (pas pour l'évaluation, cela conduira à une évaluation injuste). Essayez de faire ce changement pour le processus de formation, en assurant la
dataset_split_fnpour l' évaluation des données conserve encore la reconstruction et la reconstruction post-disjoints. Astuce:tff.learning.reconstruction.simple_dataset_split_fnpourrait être utile.Au- dessus, nous avons produit un
tff.learning.Modelà partir d' un modèle en utilisant Kerastff.learning.reconstruction.from_keras_model. Nous pouvons également mettre en œuvre un modèle personnalisé à l' aide tensorflow pur 2.0 en implémentant l'interface modèle . Essayez de modifierget_matrix_factorization_modelà construire et à retourner une classe qui étendtff.learning.reconstruction.Model, la mise en œuvre de ses méthodes. Astuce: le code source detff.learning.reconstruction.from_keras_modelfournit un exemple d'extension de latff.learning.reconstruction.Modelclasse. Se référer également à la mise entff.learning.Modelœuvre du modèle personnalisé dans le tutoriel de classification d'images EMNIST pour un exercice similaire à l' extension d' untff.learning.Model.Dans ce didacticiel, nous avons motivé l'apprentissage fédéré partiellement local dans le contexte de la factorisation matricielle, où l'envoi d'intégrations utilisateur au serveur entraînerait une fuite triviale des préférences de l'utilisateur. Nous pouvons également appliquer la reconstruction fédérée dans d'autres contextes comme moyen de former des modèles plus personnels (puisqu'une partie du modèle est complètement locale pour chaque utilisateur) tout en réduisant la communication (puisque les paramètres locaux ne sont pas envoyés au serveur). En général, en utilisant l'interface présentée ici, nous pouvons prendre n'importe quel modèle fédéré qui serait généralement entraîné de manière entièrement globale et à la place partitionner ses variables en variables globales et en variables locales. L'exemple exploré dans le papier de reconstruction fédérée est la prédiction du mot suivant personnel: ici, chaque utilisateur a son propre ensemble local de mot incorporations pour hors-vocabulaire des mots, ce qui permet au modèle de l'argot des utilisateurs de capture et d' atteindre la personnalisation sans communication supplémentaire. À titre d'exercice, essayez d'implémenter (en tant que modèle Keras ou modèle TensorFlow 2.0 personnalisé) un modèle différent à utiliser avec la reconstruction fédérée. Une suggestion : implémentez un modèle de classification EMNIST avec une intégration d'utilisateur personnel, où l'intégration d'utilisateur personnel est concaténée aux caractéristiques de l'image CNN avant la dernière couche dense du modèle. Vous pouvez réutiliser une grande partie du code à partir de ce tutoriel (par exemple , la
UserEmbeddingclasse) et l' image de classification tutoriel .
Si vous cherchez encore plus sur l' apprentissage fédérée partiellement locale, consultez le papier de reconstruction fédérée et le code de test open source .
