 Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
Hướng dẫn này sẽ trình bày phương pháp thực hành tốt nhất được đề xuất cho các mô hình đào tạo với Quyền riêng tư khác biệt ở cấp độ người dùng bằng cách sử dụng Tensorflow Federated. Chúng tôi sẽ sử dụng các thuật toán DP-SGD của Abadi et al., "Deep Learning với Differential Bảo mật" sửa đổi cho người dùng cấp DP trong một bối cảnh liên trong McMahan et al., "Học theo kiểu khác Private tái diễn Ngôn ngữ Mô hình" .
Quyền riêng tư khác biệt (DP) là một phương pháp được sử dụng rộng rãi để giới hạn và định lượng sự rò rỉ quyền riêng tư của dữ liệu nhạy cảm khi thực hiện các nhiệm vụ học tập. Việc đào tạo một mô hình với DP cấp người dùng đảm bảo rằng mô hình không có khả năng học được bất kỳ điều gì quan trọng về dữ liệu của bất kỳ cá nhân nào, nhưng vẫn có thể (hy vọng!) Học được các mẫu tồn tại trong dữ liệu của nhiều máy khách.
Chúng tôi sẽ đào tạo một mô hình trên tập dữ liệu EMNIST được liên kết. Có một sự đánh đổi cố hữu giữa tiện ích và quyền riêng tư, và có thể khó đào tạo một mô hình có tính riêng tư cao hoạt động tốt như một mô hình phi tư nhân tiên tiến nhất. Để đạt được hiệu quả trong hướng dẫn này, chúng tôi sẽ đào tạo chỉ trong 100 vòng, hy sinh một số chất lượng để chứng minh cách đào tạo với tính riêng tư cao. Nếu chúng tôi sử dụng nhiều vòng huấn luyện hơn, chúng tôi chắc chắn có thể có một mô hình riêng có độ chính xác cao hơn một chút, nhưng không cao bằng một mô hình được huấn luyện mà không có DP.
Trước khi chúng tôi bắt đầu
Trước tiên, hãy đảm bảo sổ ghi chép được kết nối với một chương trình phụ trợ có các thành phần liên quan được biên dịch.
!pip install --quiet --upgrade tensorflow_federated_nightly
!pip install --quiet --upgrade nest-asyncio
import nest_asyncio
nest_asyncio.apply()
Một số nhập khẩu mà chúng tôi sẽ cần cho phần hướng dẫn. Chúng tôi sẽ sử dụng tensorflow_federated , các framework mã nguồn mở cho máy học và tính toán khác trên dữ liệu phân cấp, cũng như tensorflow_privacy , thư viện mã nguồn mở để thực hiện và phân tích các thuật toán theo kiểu khác tin trong tensorflow.
import collections
import numpy as np
import pandas as pd
import tensorflow as tf
import tensorflow_federated as tff
import tensorflow_privacy as tfp
Chạy ví dụ "Hello World" sau đây để đảm bảo rằng môi trường TFF được thiết lập chính xác. Nếu nó không hoạt động, vui lòng tham khảo các cài đặt hướng dẫn để được hướng dẫn.
@tff.federated_computation
def hello_world():
return 'Hello, World!'
hello_world()
b'Hello, World!'
Tải xuống và xử lý trước tập dữ liệu EMNIST được liên kết.
def get_emnist_dataset():
emnist_train, emnist_test = tff.simulation.datasets.emnist.load_data(
only_digits=True)
def element_fn(element):
return collections.OrderedDict(
x=tf.expand_dims(element['pixels'], -1), y=element['label'])
def preprocess_train_dataset(dataset):
# Use buffer_size same as the maximum client dataset size,
# 418 for Federated EMNIST
return (dataset.map(element_fn)
.shuffle(buffer_size=418)
.repeat(1)
.batch(32, drop_remainder=False))
def preprocess_test_dataset(dataset):
return dataset.map(element_fn).batch(128, drop_remainder=False)
emnist_train = emnist_train.preprocess(preprocess_train_dataset)
emnist_test = preprocess_test_dataset(
emnist_test.create_tf_dataset_from_all_clients())
return emnist_train, emnist_test
train_data, test_data = get_emnist_dataset()
Xác định mô hình của chúng tôi.
def my_model_fn():
model = tf.keras.models.Sequential([
tf.keras.layers.Reshape(input_shape=(28, 28, 1), target_shape=(28 * 28,)),
tf.keras.layers.Dense(200, activation=tf.nn.relu),
tf.keras.layers.Dense(200, activation=tf.nn.relu),
tf.keras.layers.Dense(10)])
return tff.learning.from_keras_model(
keras_model=model,
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
input_spec=test_data.element_spec,
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()])
Xác định độ nhạy nhiễu của mô hình.
Để nhận được đảm bảo DP ở cấp độ người dùng, chúng ta phải thay đổi thuật toán Trung bình liên kết cơ bản theo hai cách. Đầu tiên, các bản cập nhật mô hình của máy khách phải được cắt bớt trước khi truyền đến máy chủ, giới hạn ảnh hưởng tối đa của bất kỳ máy khách nào. Thứ hai, máy chủ phải thêm đủ tiếng ồn vào tổng số lần cập nhật của người dùng trước khi tính trung bình để che khuất ảnh hưởng của máy khách trong trường hợp xấu nhất.
Đối với cắt, chúng tôi sử dụng phương pháp cắt thích nghi của Andrew et al. Năm 2021, theo kiểu khác Private Learning với thích ứng Clipping , vì vậy không cần định mức cắt được thiết lập một cách rõ ràng.
Nói chung, thêm tiếng ồn sẽ làm giảm tiện ích của mô hình, nhưng chúng tôi có thể kiểm soát lượng nhiễu trong bản cập nhật trung bình ở mỗi vòng bằng hai nút: độ lệch chuẩn của tiếng ồn Gaussian được thêm vào tổng và số lượng khách hàng trong Trung bình cộng. Chiến lược của chúng tôi trước tiên sẽ là xác định mức độ ồn mà mô hình có thể chịu đựng với một số lượng tương đối nhỏ khách hàng mỗi vòng với mức độ mất mát có thể chấp nhận được đối với tiện ích mô hình. Sau đó, để đào tạo mô hình cuối cùng, chúng ta có thể tăng tổng lượng nhiễu trong khi tăng tỷ lệ số lượng khách hàng trên mỗi vòng (giả sử tập dữ liệu đủ lớn để hỗ trợ nhiều khách hàng đó trên mỗi vòng). Điều này không có khả năng ảnh hưởng đáng kể đến chất lượng mô hình, vì tác dụng duy nhất là giảm phương sai do lấy mẫu khách hàng (thực sự chúng tôi sẽ xác minh rằng điều đó không xảy ra trong trường hợp của chúng tôi).
Để đạt được mục tiêu đó, trước tiên chúng tôi đào tạo một loạt các mô hình với 50 khách hàng mỗi vòng, với lượng tiếng ồn ngày càng tăng. Cụ thể, chúng tôi tăng "noise_multiplier", là tỷ lệ giữa độ lệch chuẩn tiếng ồn với định mức cắt. Vì chúng tôi đang sử dụng phương pháp cắt thích ứng, điều này có nghĩa là cường độ thực tế của tiếng ồn thay đổi từ vòng này sang vòng khác.
# Run five clients per thread. Increase this if your runtime is running out of
# memory. Decrease it if you have the resources and want to speed up execution.
tff.backends.native.set_local_python_execution_context(clients_per_thread=5)
total_clients = len(train_data.client_ids)
def train(rounds, noise_multiplier, clients_per_round, data_frame):
# Using the `dp_aggregator` here turns on differential privacy with adaptive
# clipping.
aggregation_factory = tff.learning.model_update_aggregator.dp_aggregator(
noise_multiplier, clients_per_round)
# We use Poisson subsampling which gives slightly tighter privacy guarantees
# compared to having a fixed number of clients per round. The actual number of
# clients per round is stochastic with mean clients_per_round.
sampling_prob = clients_per_round / total_clients
# Build a federated averaging process.
# Typically a non-adaptive server optimizer is used because the noise in the
# updates can cause the second moment accumulators to become very large
# prematurely.
learning_process = tff.learning.build_federated_averaging_process(
my_model_fn,
client_optimizer_fn=lambda: tf.keras.optimizers.SGD(0.01),
server_optimizer_fn=lambda: tf.keras.optimizers.SGD(1.0, momentum=0.9),
model_update_aggregation_factory=aggregation_factory)
eval_process = tff.learning.build_federated_evaluation(my_model_fn)
# Training loop.
state = learning_process.initialize()
for round in range(rounds):
if round % 5 == 0:
metrics = eval_process(state.model, [test_data])['eval']
if round < 25 or round % 25 == 0:
print(f'Round {round:3d}: {metrics}')
data_frame = data_frame.append({'Round': round,
'NoiseMultiplier': noise_multiplier,
**metrics}, ignore_index=True)
# Sample clients for a round. Note that if your dataset is large and
# sampling_prob is small, it would be faster to use gap sampling.
x = np.random.uniform(size=total_clients)
sampled_clients = [
train_data.client_ids[i] for i in range(total_clients)
if x[i] < sampling_prob]
sampled_train_data = [
train_data.create_tf_dataset_for_client(client)
for client in sampled_clients]
# Use selected clients for update.
state, metrics = learning_process.next(state, sampled_train_data)
metrics = eval_process(state.model, [test_data])['eval']
print(f'Round {rounds:3d}: {metrics}')
data_frame = data_frame.append({'Round': rounds,
'NoiseMultiplier': noise_multiplier,
**metrics}, ignore_index=True)
return data_frame
data_frame = pd.DataFrame()
rounds = 100
clients_per_round = 50
for noise_multiplier in [0.0, 0.5, 0.75, 1.0]:
print(f'Starting training with noise multiplier: {noise_multiplier}')
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
print()
Starting training with noise multiplier: 0.0
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.112289384), ('loss', 2.5190482)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.19075724), ('loss', 2.2449977)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.18115693), ('loss', 2.163907)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.49970612), ('loss', 2.01017)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5333317), ('loss', 1.8350543)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.5828517), ('loss', 1.6551636)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.7352077), ('loss', 0.8700141)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.7769152), ('loss', 0.6992781)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.8049814), ('loss', 0.62453026)])
Starting training with noise multiplier: 0.5
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.09526841), ('loss', 2.4332638)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.20128821), ('loss', 2.2664592)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.35472178), ('loss', 2.130336)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.5480995), ('loss', 1.9713942)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.42246276), ('loss', 1.8045483)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.624902), ('loss', 1.4785467)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.7265625), ('loss', 0.85801566)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.77720904), ('loss', 0.70615387)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7702537), ('loss', 0.72331005)])
Starting training with noise multiplier: 0.75
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.098672606), ('loss', 2.422002)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.11794671), ('loss', 2.2227976)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.3208513), ('loss', 2.083766)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.49752644), ('loss', 1.8728142)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5816761), ('loss', 1.6084186)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.62896746), ('loss', 1.378527)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.73153406), ('loss', 0.8705139)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.7789724), ('loss', 0.7113147)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.70944357), ('loss', 0.89495045)])
Starting training with noise multiplier: 1.0
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.12002841), ('loss', 2.60482)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.104574844), ('loss', 2.3388205)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.29966694), ('loss', 2.089262)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.4067398), ('loss', 1.9109797)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5123677), ('loss', 1.6472703)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.56416535), ('loss', 1.4362282)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.62323666), ('loss', 1.1682972)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.55968356), ('loss', 1.4779186)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.382837), ('loss', 1.9680436)])
Bây giờ chúng ta có thể hình dung độ chính xác của bộ đánh giá và mất mát của những lần chạy đó.
import matplotlib.pyplot as plt
import seaborn as sns
def make_plot(data_frame):
plt.figure(figsize=(15, 5))
dff = data_frame.rename(
columns={'sparse_categorical_accuracy': 'Accuracy', 'loss': 'Loss'})
plt.subplot(121)
sns.lineplot(data=dff, x='Round', y='Accuracy', hue='NoiseMultiplier', palette='dark')
plt.subplot(122)
sns.lineplot(data=dff, x='Round', y='Loss', hue='NoiseMultiplier', palette='dark')
make_plot(data_frame)
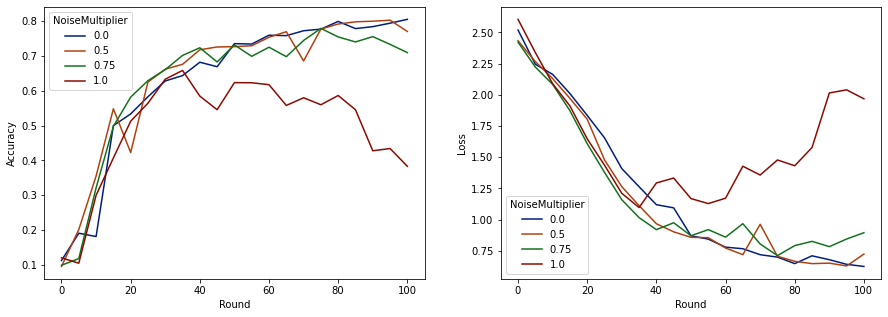
Dường như với 50 khách hàng dự kiến mỗi vòng, mô hình này có thể chịu được hệ số nhiễu lên đến 0,5 mà không làm giảm chất lượng mô hình. Hệ số nhiễu 0,75 dường như gây ra một chút suy giảm mô hình và 1,0 làm cho mô hình phân kỳ.
Thường có sự cân bằng giữa chất lượng mô hình và quyền riêng tư. Tiếng ồn chúng tôi sử dụng càng cao, chúng tôi càng có được nhiều quyền riêng tư hơn với cùng một lượng thời gian đào tạo và số lượng khách hàng. Ngược lại, với ít tiếng ồn hơn, chúng tôi có thể có một mô hình chính xác hơn, nhưng chúng tôi sẽ phải đào tạo với nhiều khách hàng hơn mỗi vòng để đạt được mức độ riêng tư mục tiêu của chúng tôi.
Với thử nghiệm ở trên, chúng tôi có thể quyết định rằng mức độ suy giảm nhỏ của mô hình ở mức 0,75 là có thể chấp nhận được để đào tạo mô hình cuối cùng nhanh hơn, nhưng giả sử chúng tôi muốn phù hợp với hiệu suất của mô hình hệ số nhiễu 0,5.
Giờ đây, chúng tôi có thể sử dụng các chức năng tensorflow_privacy để xác định số lượng khách hàng mong đợi mỗi vòng mà chúng tôi sẽ cần để có được sự riêng tư có thể chấp nhận được. Thực hành tiêu chuẩn là chọn delta nhỏ hơn một chút so với số lượng bản ghi trong tập dữ liệu. Tập dữ liệu này có tổng số 3383 người dùng đào tạo, vì vậy hãy nhắm đến (2, 1e-5) -DP.
Chúng tôi sử dụng một tìm kiếm nhị phân đơn giản về số lượng khách hàng mỗi vòng. Chức năng tensorflow_privacy chúng tôi sử dụng để ước tính epsilon được dựa trên Wang et al. (2018) và Mironov et al. (2019) .
rdp_orders = ([1.25, 1.5, 1.75, 2., 2.25, 2.5, 3., 3.5, 4., 4.5] +
list(range(5, 64)) + [128, 256, 512])
total_clients = 3383
base_noise_multiplier = 0.5
base_clients_per_round = 50
target_delta = 1e-5
target_eps = 2
def get_epsilon(clients_per_round):
# If we use this number of clients per round and proportionally
# scale up the noise multiplier, what epsilon do we achieve?
q = clients_per_round / total_clients
noise_multiplier = base_noise_multiplier
noise_multiplier *= clients_per_round / base_clients_per_round
rdp = tfp.compute_rdp(
q, noise_multiplier=noise_multiplier, steps=rounds, orders=rdp_orders)
eps, _, _ = tfp.get_privacy_spent(rdp_orders, rdp, target_delta=target_delta)
return clients_per_round, eps, noise_multiplier
def find_needed_clients_per_round():
hi = get_epsilon(base_clients_per_round)
if hi[1] < target_eps:
return hi
# Grow interval exponentially until target_eps is exceeded.
while True:
lo = hi
hi = get_epsilon(2 * lo[0])
if hi[1] < target_eps:
break
# Binary search.
while hi[0] - lo[0] > 1:
mid = get_epsilon((lo[0] + hi[0]) // 2)
if mid[1] > target_eps:
lo = mid
else:
hi = mid
return hi
clients_per_round, _, noise_multiplier = find_needed_clients_per_round()
print(f'To get ({target_eps}, {target_delta})-DP, use {clients_per_round} '
f'clients with noise multiplier {noise_multiplier}.')
To get (2, 1e-05)-DP, use 120 clients with noise multiplier 1.2.
Bây giờ chúng tôi có thể đào tạo mô hình riêng tư cuối cùng của chúng tôi để phát hành.
rounds = 100
noise_multiplier = 1.2
clients_per_round = 120
data_frame = pd.DataFrame()
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
make_plot(data_frame)
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.08260678), ('loss', 2.6334999)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.1492212), ('loss', 2.259542)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.28847474), ('loss', 2.155699)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.3989518), ('loss', 2.0156953)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5086697), ('loss', 1.8261365)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.6204692), ('loss', 1.5602393)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.70008814), ('loss', 0.91155165)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.78421336), ('loss', 0.6820159)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7955525), ('loss', 0.6585961)])
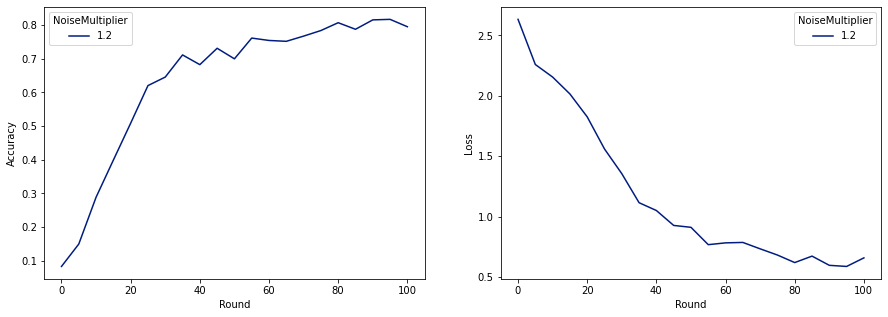
Như chúng ta có thể thấy, mô hình cuối cùng có độ hao hụt và độ chính xác tương tự với mô hình được huấn luyện không nhiễu, nhưng mô hình này thỏa mãn (2, 1e-5) -DP.
