 ดูบน TensorFlow.org ดูบน TensorFlow.org |  ทำงานใน Google Colab ทำงานใน Google Colab |  ดูแหล่งที่มาบน GitHub ดูแหล่งที่มาบน GitHub |  ดาวน์โหลดโน๊ตบุ๊ค ดาวน์โหลดโน๊ตบุ๊ค |
บทช่วยสอนนี้จะสาธิตแนวทางปฏิบัติที่ดีที่สุดที่แนะนำสำหรับโมเดลการฝึกอบรมที่มี Differential Privacy ระดับผู้ใช้โดยใช้ Tensorflow Federated เราจะใช้อัลกอริทึม DP-SGD ของ Abadi et al., "การเรียนรู้ลึกที่มีความแตกต่างของความเป็นส่วนตัว" การปรับเปลี่ยนสำหรับผู้ใช้ระดับ DP ในบริบทสหพันธ์ McMahan et al., "การเรียนรู้ Differentially เอกชนกำเริบภาษารุ่น"
Differential Privacy (DP) เป็นวิธีที่ใช้กันอย่างแพร่หลายในการจำกัดและวัดปริมาณการรั่วไหลของความเป็นส่วนตัวของข้อมูลที่ละเอียดอ่อนเมื่อดำเนินการเรียนรู้ การฝึกโมเดลด้วย DP ระดับผู้ใช้รับประกันว่าโมเดลไม่น่าจะเรียนรู้อะไรที่สำคัญเกี่ยวกับข้อมูลของบุคคลใด ๆ แต่ยังสามารถ (หวังว่า!) เรียนรู้รูปแบบที่มีอยู่ในข้อมูลของลูกค้าจำนวนมาก
เราจะฝึกแบบจำลองบนชุดข้อมูล EMNIST แบบรวมศูนย์ มีการแลกเปลี่ยนโดยธรรมชาติระหว่างยูทิลิตี้และความเป็นส่วนตัว และอาจเป็นเรื่องยากที่จะฝึกแบบจำลองที่มีความเป็นส่วนตัวสูงซึ่งทำงานได้ดีพอ ๆ กับแบบจำลองที่ไม่ใช่ส่วนตัวที่ล้ำสมัย เพื่อความได้เปรียบในบทช่วยสอนนี้ เราจะฝึกเพียง 100 รอบ โดยสละคุณภาพบางส่วนเพื่อสาธิตวิธีการฝึกอบรมที่มีความเป็นส่วนตัวสูง หากเราใช้รอบการฝึกมากขึ้น เราก็อาจมีโมเดลส่วนตัวที่มีความแม่นยำสูงกว่า แต่ก็ไม่สูงเท่าโมเดลที่ฝึกโดยไม่มี DP
ก่อนที่เราจะเริ่มต้น
อันดับแรก ให้เราตรวจสอบให้แน่ใจว่าโน้ตบุ๊กเชื่อมต่อกับแบ็กเอนด์ที่มีการรวบรวมส่วนประกอบที่เกี่ยวข้อง
!pip install --quiet --upgrade tensorflow_federated_nightly
!pip install --quiet --upgrade nest-asyncio
import nest_asyncio
nest_asyncio.apply()
เราจะต้องนำเข้าบางส่วนสำหรับบทช่วยสอน เราจะใช้ tensorflow_federated กรอบเปิดแหล่งที่มาสำหรับการเรียนรู้และการคำนวณเครื่องอื่น ๆ เกี่ยวกับข้อมูลการกระจายอำนาจเช่นเดียวกับ tensorflow_privacy ห้องสมุดเปิดแหล่งที่มาสำหรับการดำเนินการและการวิเคราะห์ขั้นตอนวิธีการที่แตกต่างกันในส่วนตัว tensorflow
import collections
import numpy as np
import pandas as pd
import tensorflow as tf
import tensorflow_federated as tff
import tensorflow_privacy as tfp
เรียกใช้ตัวอย่าง "Hello World" ต่อไปนี้เพื่อให้แน่ใจว่าสภาพแวดล้อม TFF ได้รับการตั้งค่าอย่างถูกต้อง ถ้ามันไม่ทำงานโปรดดูที่ การติดตั้ง คู่มือสำหรับคำแนะนำ
@tff.federated_computation
def hello_world():
return 'Hello, World!'
hello_world()
b'Hello, World!'
ดาวน์โหลดและประมวลผลชุดข้อมูล EMNIST แบบรวมศูนย์ล่วงหน้า
def get_emnist_dataset():
emnist_train, emnist_test = tff.simulation.datasets.emnist.load_data(
only_digits=True)
def element_fn(element):
return collections.OrderedDict(
x=tf.expand_dims(element['pixels'], -1), y=element['label'])
def preprocess_train_dataset(dataset):
# Use buffer_size same as the maximum client dataset size,
# 418 for Federated EMNIST
return (dataset.map(element_fn)
.shuffle(buffer_size=418)
.repeat(1)
.batch(32, drop_remainder=False))
def preprocess_test_dataset(dataset):
return dataset.map(element_fn).batch(128, drop_remainder=False)
emnist_train = emnist_train.preprocess(preprocess_train_dataset)
emnist_test = preprocess_test_dataset(
emnist_test.create_tf_dataset_from_all_clients())
return emnist_train, emnist_test
train_data, test_data = get_emnist_dataset()
กำหนดรูปแบบของเรา
def my_model_fn():
model = tf.keras.models.Sequential([
tf.keras.layers.Reshape(input_shape=(28, 28, 1), target_shape=(28 * 28,)),
tf.keras.layers.Dense(200, activation=tf.nn.relu),
tf.keras.layers.Dense(200, activation=tf.nn.relu),
tf.keras.layers.Dense(10)])
return tff.learning.from_keras_model(
keras_model=model,
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
input_spec=test_data.element_spec,
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()])
กำหนดความไวของสัญญาณรบกวนของแบบจำลอง
ในการรับการรับประกัน DP ระดับผู้ใช้ เราต้องเปลี่ยนอัลกอริธึม Federated Averaging พื้นฐานในสองวิธี ประการแรก การอัปเดตโมเดลของไคลเอ็นต์ต้องถูกตัดออกก่อนที่จะส่งไปยังเซิร์ฟเวอร์ โดยจำกัดอิทธิพลสูงสุดของไคลเอ็นต์รายใดรายหนึ่ง ประการที่สอง เซิร์ฟเวอร์ต้องเพิ่มสัญญาณรบกวนที่เพียงพอให้กับผลรวมของการอัปเดตผู้ใช้ก่อนที่จะหาค่าเฉลี่ยเพื่อบดบังอิทธิพลของไคลเอ็นต์ในกรณีที่แย่ที่สุด
สำหรับการตัดเราจะใช้วิธีการตัดการปรับตัวของ แอนดรู, et al 2021 Differentially การเรียนรู้ส่วนตัวที่มีการปรับเปลี่ยนรูปวาด จึงไม่มีความต้องการตัดบรรทัดฐานที่จะกำหนดอย่างชัดเจน
การเพิ่มเสียงรบกวนโดยทั่วไปจะทำให้ยูทิลิตี้ของโมเดลลดลง แต่เราสามารถควบคุมปริมาณเสียงรบกวนในการอัพเดทโดยเฉลี่ยในแต่ละรอบด้วยปุ่มสองปุ่ม: ค่าเบี่ยงเบนมาตรฐานของเสียงรบกวนแบบเกาส์เซียนที่เพิ่มเข้าไปในผลรวม และจำนวนไคลเอนต์ใน เฉลี่ย. กลยุทธ์ของเราคือการพิจารณาก่อนว่าโมเดลสามารถทนต่อเสียงรบกวนได้มากน้อยเพียงใดโดยมีลูกค้าจำนวนค่อนข้างน้อยต่อรอบโดยสูญเสียยูทิลิตี้โมเดลที่ยอมรับได้ จากนั้นในการฝึกโมเดลสุดท้าย เราสามารถเพิ่มปริมาณของสัญญาณรบกวนในผลรวม ในขณะที่ขยายจำนวนไคลเอนต์ต่อรอบตามสัดส่วน (สมมติว่าชุดข้อมูลมีขนาดใหญ่พอที่จะรองรับไคลเอนต์จำนวนมากต่อรอบ) สิ่งนี้ไม่น่าจะส่งผลกระทบอย่างมีนัยสำคัญต่อคุณภาพของแบบจำลอง เนื่องจากผลกระทบเพียงอย่างเดียวคือการลดความแปรปรวนเนื่องจากการสุ่มตัวอย่างของลูกค้า
ด้วยเหตุนี้ ขั้นแรก เราจึงฝึกรุ่นต่างๆ ของโมเดลโดยมีไคลเอ็นต์ 50 รายต่อรอบ โดยมีปริมาณสัญญาณรบกวนเพิ่มขึ้น โดยเฉพาะอย่างยิ่ง เราเพิ่ม "noise_multiplier" ซึ่งเป็นอัตราส่วนของค่าเบี่ยงเบนมาตรฐานของสัญญาณรบกวนต่อบรรทัดฐานของการตัดทอน เนื่องจากเราใช้การตัดแบบปรับได้ ซึ่งหมายความว่าขนาดที่แท้จริงของเสียงจะเปลี่ยนแปลงจากรอบหนึ่งไปอีกรอบ
# Run five clients per thread. Increase this if your runtime is running out of
# memory. Decrease it if you have the resources and want to speed up execution.
tff.backends.native.set_local_python_execution_context(clients_per_thread=5)
total_clients = len(train_data.client_ids)
def train(rounds, noise_multiplier, clients_per_round, data_frame):
# Using the `dp_aggregator` here turns on differential privacy with adaptive
# clipping.
aggregation_factory = tff.learning.model_update_aggregator.dp_aggregator(
noise_multiplier, clients_per_round)
# We use Poisson subsampling which gives slightly tighter privacy guarantees
# compared to having a fixed number of clients per round. The actual number of
# clients per round is stochastic with mean clients_per_round.
sampling_prob = clients_per_round / total_clients
# Build a federated averaging process.
# Typically a non-adaptive server optimizer is used because the noise in the
# updates can cause the second moment accumulators to become very large
# prematurely.
learning_process = tff.learning.build_federated_averaging_process(
my_model_fn,
client_optimizer_fn=lambda: tf.keras.optimizers.SGD(0.01),
server_optimizer_fn=lambda: tf.keras.optimizers.SGD(1.0, momentum=0.9),
model_update_aggregation_factory=aggregation_factory)
eval_process = tff.learning.build_federated_evaluation(my_model_fn)
# Training loop.
state = learning_process.initialize()
for round in range(rounds):
if round % 5 == 0:
metrics = eval_process(state.model, [test_data])['eval']
if round < 25 or round % 25 == 0:
print(f'Round {round:3d}: {metrics}')
data_frame = data_frame.append({'Round': round,
'NoiseMultiplier': noise_multiplier,
**metrics}, ignore_index=True)
# Sample clients for a round. Note that if your dataset is large and
# sampling_prob is small, it would be faster to use gap sampling.
x = np.random.uniform(size=total_clients)
sampled_clients = [
train_data.client_ids[i] for i in range(total_clients)
if x[i] < sampling_prob]
sampled_train_data = [
train_data.create_tf_dataset_for_client(client)
for client in sampled_clients]
# Use selected clients for update.
state, metrics = learning_process.next(state, sampled_train_data)
metrics = eval_process(state.model, [test_data])['eval']
print(f'Round {rounds:3d}: {metrics}')
data_frame = data_frame.append({'Round': rounds,
'NoiseMultiplier': noise_multiplier,
**metrics}, ignore_index=True)
return data_frame
data_frame = pd.DataFrame()
rounds = 100
clients_per_round = 50
for noise_multiplier in [0.0, 0.5, 0.75, 1.0]:
print(f'Starting training with noise multiplier: {noise_multiplier}')
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
print()
Starting training with noise multiplier: 0.0
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.112289384), ('loss', 2.5190482)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.19075724), ('loss', 2.2449977)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.18115693), ('loss', 2.163907)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.49970612), ('loss', 2.01017)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5333317), ('loss', 1.8350543)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.5828517), ('loss', 1.6551636)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.7352077), ('loss', 0.8700141)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.7769152), ('loss', 0.6992781)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.8049814), ('loss', 0.62453026)])
Starting training with noise multiplier: 0.5
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.09526841), ('loss', 2.4332638)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.20128821), ('loss', 2.2664592)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.35472178), ('loss', 2.130336)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.5480995), ('loss', 1.9713942)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.42246276), ('loss', 1.8045483)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.624902), ('loss', 1.4785467)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.7265625), ('loss', 0.85801566)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.77720904), ('loss', 0.70615387)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7702537), ('loss', 0.72331005)])
Starting training with noise multiplier: 0.75
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.098672606), ('loss', 2.422002)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.11794671), ('loss', 2.2227976)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.3208513), ('loss', 2.083766)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.49752644), ('loss', 1.8728142)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5816761), ('loss', 1.6084186)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.62896746), ('loss', 1.378527)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.73153406), ('loss', 0.8705139)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.7789724), ('loss', 0.7113147)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.70944357), ('loss', 0.89495045)])
Starting training with noise multiplier: 1.0
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.12002841), ('loss', 2.60482)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.104574844), ('loss', 2.3388205)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.29966694), ('loss', 2.089262)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.4067398), ('loss', 1.9109797)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5123677), ('loss', 1.6472703)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.56416535), ('loss', 1.4362282)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.62323666), ('loss', 1.1682972)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.55968356), ('loss', 1.4779186)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.382837), ('loss', 1.9680436)])
ตอนนี้เราสามารถเห็นภาพความถูกต้องของชุดการประเมินและการสูญเสียของการรันเหล่านั้น
import matplotlib.pyplot as plt
import seaborn as sns
def make_plot(data_frame):
plt.figure(figsize=(15, 5))
dff = data_frame.rename(
columns={'sparse_categorical_accuracy': 'Accuracy', 'loss': 'Loss'})
plt.subplot(121)
sns.lineplot(data=dff, x='Round', y='Accuracy', hue='NoiseMultiplier', palette='dark')
plt.subplot(122)
sns.lineplot(data=dff, x='Round', y='Loss', hue='NoiseMultiplier', palette='dark')
make_plot(data_frame)
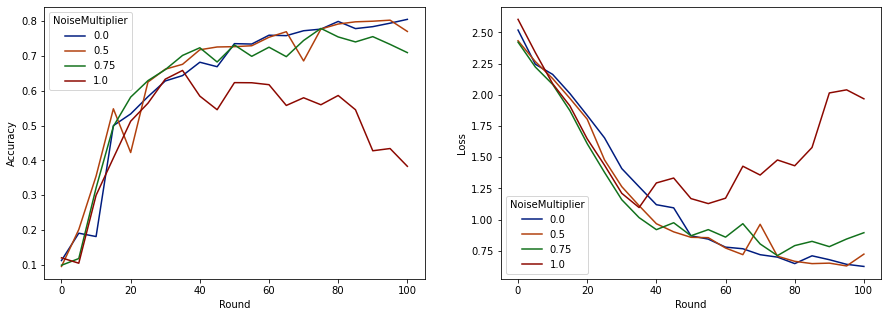
ปรากฏว่ามีลูกค้าคาดหวัง 50 รายต่อรอบ โมเดลนี้สามารถทนต่อตัวคูณเสียงรบกวนได้สูงถึง 0.5 โดยไม่ลดคุณภาพของโมเดล ตัวคูณสัญญาณรบกวน 0.75 ดูเหมือนจะทำให้โมเดลเสื่อมโทรมเล็กน้อย และ 1.0 ทำให้โมเดลแตกต่างออกไป
โดยทั่วไปจะมีการแลกเปลี่ยนระหว่างคุณภาพของแบบจำลองและความเป็นส่วนตัว ยิ่งเราใช้เสียงรบกวนมากเท่าไร เราก็ยิ่งได้รับความเป็นส่วนตัวมากขึ้นเท่านั้นสำหรับเวลาการฝึกอบรมและจำนวนลูกค้าที่เท่ากัน ในทางกลับกัน หากเสียงรบกวนน้อยลง เราอาจมีโมเดลที่แม่นยำกว่า แต่เราจะต้องฝึกอบรมกับลูกค้ามากขึ้นในแต่ละรอบเพื่อให้ถึงระดับความเป็นส่วนตัวเป้าหมายของเรา
จากการทดลองข้างต้น เราอาจตัดสินใจว่าการเสื่อมสภาพของแบบจำลองจำนวนเล็กน้อยที่ 0.75 นั้นเป็นที่ยอมรับได้ เพื่อที่จะฝึกโมเดลสุดท้ายให้เร็วขึ้น แต่สมมติว่าเราต้องการจับคู่ประสิทธิภาพของโมเดลตัวคูณสัญญาณรบกวน 0.5
ตอนนี้ เราสามารถใช้ฟังก์ชัน tensorflow_privacy เพื่อกำหนดจำนวนลูกค้าที่คาดหวังต่อรอบ เราจะต้องได้รับความเป็นส่วนตัวที่ยอมรับได้ แนวปฏิบัติมาตรฐานคือการเลือกเดลต้าที่ค่อนข้างเล็กกว่าหนึ่งในจำนวนเร็กคอร์ดในชุดข้อมูล ชุดข้อมูลนี้มีผู้ใช้การฝึกทั้งหมด 3383 คน ดังนั้นเรามาตั้งเป้า (2, 1e-5)-DP กัน
เราใช้การค้นหาแบบไบนารีอย่างง่ายกับจำนวนลูกค้าต่อรอบ ฟังก์ชั่น tensorflow_privacy เราใช้ในการประเมิน epsilon จะขึ้นอยู่กับ วัง et al, (2018) และ Mironov et al, (2019)
rdp_orders = ([1.25, 1.5, 1.75, 2., 2.25, 2.5, 3., 3.5, 4., 4.5] +
list(range(5, 64)) + [128, 256, 512])
total_clients = 3383
base_noise_multiplier = 0.5
base_clients_per_round = 50
target_delta = 1e-5
target_eps = 2
def get_epsilon(clients_per_round):
# If we use this number of clients per round and proportionally
# scale up the noise multiplier, what epsilon do we achieve?
q = clients_per_round / total_clients
noise_multiplier = base_noise_multiplier
noise_multiplier *= clients_per_round / base_clients_per_round
rdp = tfp.compute_rdp(
q, noise_multiplier=noise_multiplier, steps=rounds, orders=rdp_orders)
eps, _, _ = tfp.get_privacy_spent(rdp_orders, rdp, target_delta=target_delta)
return clients_per_round, eps, noise_multiplier
def find_needed_clients_per_round():
hi = get_epsilon(base_clients_per_round)
if hi[1] < target_eps:
return hi
# Grow interval exponentially until target_eps is exceeded.
while True:
lo = hi
hi = get_epsilon(2 * lo[0])
if hi[1] < target_eps:
break
# Binary search.
while hi[0] - lo[0] > 1:
mid = get_epsilon((lo[0] + hi[0]) // 2)
if mid[1] > target_eps:
lo = mid
else:
hi = mid
return hi
clients_per_round, _, noise_multiplier = find_needed_clients_per_round()
print(f'To get ({target_eps}, {target_delta})-DP, use {clients_per_round} '
f'clients with noise multiplier {noise_multiplier}.')
To get (2, 1e-05)-DP, use 120 clients with noise multiplier 1.2.
ตอนนี้ เราสามารถฝึกโมเดลส่วนตัวขั้นสุดท้ายสำหรับการเปิดตัวได้
rounds = 100
noise_multiplier = 1.2
clients_per_round = 120
data_frame = pd.DataFrame()
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
make_plot(data_frame)
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.08260678), ('loss', 2.6334999)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.1492212), ('loss', 2.259542)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.28847474), ('loss', 2.155699)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.3989518), ('loss', 2.0156953)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5086697), ('loss', 1.8261365)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.6204692), ('loss', 1.5602393)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.70008814), ('loss', 0.91155165)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.78421336), ('loss', 0.6820159)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7955525), ('loss', 0.6585961)])
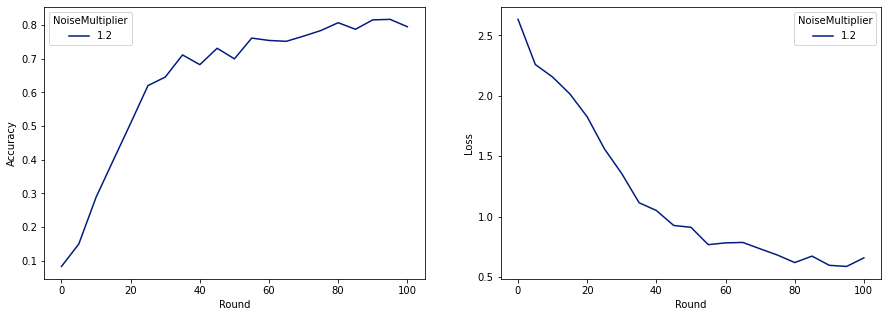
ดังที่เราเห็น โมเดลสุดท้ายมีความสูญเสียและความแม่นยำคล้ายกับรุ่นที่ฝึกโดยไม่มีเสียงรบกวน แต่รุ่นนี้ตอบสนอง (2, 1e-5)-DP
