 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
Ten samouczek zademonstruje zalecane najlepsze praktyki dotyczące modeli szkoleniowych z różnicową prywatnością na poziomie użytkownika przy użyciu Tensorflow Federated. Użyjemy algorytmu DP-SGD z Abadi et al., „Głęboka Nauka z Prywatność Differential” zmodyfikowane do poziomu użytkownika DP w stowarzyszonym w kontekście patrz praca: McMahan et al., „Learning Różnicowo Prywatna Nawracające Językowych Models” .
Prywatność różnicowa (DP) to szeroko stosowana metoda ograniczania i określania ilościowego wycieku danych wrażliwych podczas wykonywania zadań edukacyjnych. Szkolenie modelu z DP na poziomie użytkownika gwarantuje, że jest mało prawdopodobne, aby model nauczył się niczego istotnego o danych jakiejkolwiek osoby, ale nadal może (miejmy nadzieję!) nauczyć się wzorców, które istnieją w danych wielu klientów.
Będziemy trenować model na sfederowanym zbiorze danych EMNIST. Istnieje nieodłączny kompromis między użytecznością a prywatnością i może być trudno wytrenować model o wysokiej prywatności, który działa równie dobrze jak najnowocześniejszy model nieprywatny. Dla wygody w tym samouczku będziemy trenować tylko przez 100 rund, poświęcając trochę jakości, aby zademonstrować, jak trenować z dużą prywatnością. Gdybyśmy zastosowali więcej rund szkoleniowych, z pewnością moglibyśmy mieć nieco bardziej dokładny model prywatny, ale nie tak wysoki, jak model wytrenowany bez DP.
Zanim zaczniemy
Najpierw upewnijmy się, że notebook jest podłączony do zaplecza, na którym skompilowano odpowiednie komponenty.
!pip install --quiet --upgrade tensorflow_federated_nightly
!pip install --quiet --upgrade nest-asyncio
import nest_asyncio
nest_asyncio.apply()
Niektóre importy będziemy potrzebować w samouczku. Użyjemy tensorflow_federated , ramy open source dla uczenia maszynowego i innych obliczeń na zdecentralizowanych danych, jak również tensorflow_privacy , biblioteki open-source do wdrażania i analizowania algorytmów różnie prywatnych w tensorflow.
import collections
import numpy as np
import pandas as pd
import tensorflow as tf
import tensorflow_federated as tff
import tensorflow_privacy as tfp
Uruchom następujący przykład „Hello World”, aby upewnić się, że środowisko TFF jest poprawnie skonfigurowane. Jeśli to nie działa, proszę odnieść się do montażu prowadnicy do instrukcji.
@tff.federated_computation
def hello_world():
return 'Hello, World!'
hello_world()
b'Hello, World!'
Pobierz i wstępnie przetwórz sfederowany zbiór danych EMNIST.
def get_emnist_dataset():
emnist_train, emnist_test = tff.simulation.datasets.emnist.load_data(
only_digits=True)
def element_fn(element):
return collections.OrderedDict(
x=tf.expand_dims(element['pixels'], -1), y=element['label'])
def preprocess_train_dataset(dataset):
# Use buffer_size same as the maximum client dataset size,
# 418 for Federated EMNIST
return (dataset.map(element_fn)
.shuffle(buffer_size=418)
.repeat(1)
.batch(32, drop_remainder=False))
def preprocess_test_dataset(dataset):
return dataset.map(element_fn).batch(128, drop_remainder=False)
emnist_train = emnist_train.preprocess(preprocess_train_dataset)
emnist_test = preprocess_test_dataset(
emnist_test.create_tf_dataset_from_all_clients())
return emnist_train, emnist_test
train_data, test_data = get_emnist_dataset()
Zdefiniuj nasz model.
def my_model_fn():
model = tf.keras.models.Sequential([
tf.keras.layers.Reshape(input_shape=(28, 28, 1), target_shape=(28 * 28,)),
tf.keras.layers.Dense(200, activation=tf.nn.relu),
tf.keras.layers.Dense(200, activation=tf.nn.relu),
tf.keras.layers.Dense(10)])
return tff.learning.from_keras_model(
keras_model=model,
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
input_spec=test_data.element_spec,
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()])
Określ czułość modelu na hałas.
Aby uzyskać gwarancje DP na poziomie użytkownika, musimy zmienić podstawowy algorytm uśredniania federacyjnego na dwa sposoby. Po pierwsze, aktualizacje modelu klientów muszą zostać obcięte przed transmisją na serwer, ograniczając maksymalny wpływ dowolnego klienta. Po drugie, serwer musi dodać wystarczającą ilość szumu do sumy aktualizacji użytkownika przed uśrednieniem, aby ukryć wpływ klienta w najgorszym przypadku.
Do przycinania używamy adaptacyjną metodę obcinania z Andrew et al. 2021, Różnicowo Prywatna Nauka Adaptive przycinania , więc nie norma strzyżenie musi być jawnie ustawione.
Dodanie szumu ogólnie obniży użyteczność modelu, ale możemy kontrolować ilość szumu w średniej aktualizacji w każdej rundzie za pomocą dwóch pokręteł: odchylenia standardowego szumu Gaussa dodanego do sumy i liczby klientów w przeciętny. Naszą strategią będzie najpierw określenie, jak duży szum może tolerować model przy stosunkowo małej liczbie klientów na rundę, przy akceptowalnej utracie użyteczności modelu. Następnie, aby wytrenować ostateczny model, możemy zwiększyć ilość szumu w sumie, jednocześnie proporcjonalnie zwiększając liczbę klientów na rundę (zakładając, że zestaw danych jest wystarczająco duży, aby obsłużyć tylu klientów na rundę). Jest mało prawdopodobne, aby miało to znaczący wpływ na jakość modelu, ponieważ jedynym efektem jest zmniejszenie wariancji ze względu na próbkowanie klienta (w rzeczywistości zweryfikujemy, że tak nie jest w naszym przypadku).
W tym celu najpierw szkolimy serię modeli z 50 klientami na rundę, przy coraz większym hałasie. W szczególności zwiększamy „noise_multiplier”, który jest stosunkiem odchylenia standardowego szumu do normy obcinania. Ponieważ używamy adaptacyjnego przycinania, oznacza to, że rzeczywista wielkość szumu zmienia się z okrągłej na okrągłą.
# Run five clients per thread. Increase this if your runtime is running out of
# memory. Decrease it if you have the resources and want to speed up execution.
tff.backends.native.set_local_python_execution_context(clients_per_thread=5)
total_clients = len(train_data.client_ids)
def train(rounds, noise_multiplier, clients_per_round, data_frame):
# Using the `dp_aggregator` here turns on differential privacy with adaptive
# clipping.
aggregation_factory = tff.learning.model_update_aggregator.dp_aggregator(
noise_multiplier, clients_per_round)
# We use Poisson subsampling which gives slightly tighter privacy guarantees
# compared to having a fixed number of clients per round. The actual number of
# clients per round is stochastic with mean clients_per_round.
sampling_prob = clients_per_round / total_clients
# Build a federated averaging process.
# Typically a non-adaptive server optimizer is used because the noise in the
# updates can cause the second moment accumulators to become very large
# prematurely.
learning_process = tff.learning.build_federated_averaging_process(
my_model_fn,
client_optimizer_fn=lambda: tf.keras.optimizers.SGD(0.01),
server_optimizer_fn=lambda: tf.keras.optimizers.SGD(1.0, momentum=0.9),
model_update_aggregation_factory=aggregation_factory)
eval_process = tff.learning.build_federated_evaluation(my_model_fn)
# Training loop.
state = learning_process.initialize()
for round in range(rounds):
if round % 5 == 0:
metrics = eval_process(state.model, [test_data])['eval']
if round < 25 or round % 25 == 0:
print(f'Round {round:3d}: {metrics}')
data_frame = data_frame.append({'Round': round,
'NoiseMultiplier': noise_multiplier,
**metrics}, ignore_index=True)
# Sample clients for a round. Note that if your dataset is large and
# sampling_prob is small, it would be faster to use gap sampling.
x = np.random.uniform(size=total_clients)
sampled_clients = [
train_data.client_ids[i] for i in range(total_clients)
if x[i] < sampling_prob]
sampled_train_data = [
train_data.create_tf_dataset_for_client(client)
for client in sampled_clients]
# Use selected clients for update.
state, metrics = learning_process.next(state, sampled_train_data)
metrics = eval_process(state.model, [test_data])['eval']
print(f'Round {rounds:3d}: {metrics}')
data_frame = data_frame.append({'Round': rounds,
'NoiseMultiplier': noise_multiplier,
**metrics}, ignore_index=True)
return data_frame
data_frame = pd.DataFrame()
rounds = 100
clients_per_round = 50
for noise_multiplier in [0.0, 0.5, 0.75, 1.0]:
print(f'Starting training with noise multiplier: {noise_multiplier}')
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
print()
Starting training with noise multiplier: 0.0
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.112289384), ('loss', 2.5190482)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.19075724), ('loss', 2.2449977)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.18115693), ('loss', 2.163907)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.49970612), ('loss', 2.01017)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5333317), ('loss', 1.8350543)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.5828517), ('loss', 1.6551636)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.7352077), ('loss', 0.8700141)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.7769152), ('loss', 0.6992781)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.8049814), ('loss', 0.62453026)])
Starting training with noise multiplier: 0.5
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.09526841), ('loss', 2.4332638)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.20128821), ('loss', 2.2664592)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.35472178), ('loss', 2.130336)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.5480995), ('loss', 1.9713942)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.42246276), ('loss', 1.8045483)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.624902), ('loss', 1.4785467)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.7265625), ('loss', 0.85801566)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.77720904), ('loss', 0.70615387)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7702537), ('loss', 0.72331005)])
Starting training with noise multiplier: 0.75
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.098672606), ('loss', 2.422002)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.11794671), ('loss', 2.2227976)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.3208513), ('loss', 2.083766)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.49752644), ('loss', 1.8728142)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5816761), ('loss', 1.6084186)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.62896746), ('loss', 1.378527)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.73153406), ('loss', 0.8705139)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.7789724), ('loss', 0.7113147)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.70944357), ('loss', 0.89495045)])
Starting training with noise multiplier: 1.0
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.12002841), ('loss', 2.60482)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.104574844), ('loss', 2.3388205)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.29966694), ('loss', 2.089262)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.4067398), ('loss', 1.9109797)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5123677), ('loss', 1.6472703)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.56416535), ('loss', 1.4362282)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.62323666), ('loss', 1.1682972)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.55968356), ('loss', 1.4779186)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.382837), ('loss', 1.9680436)])
Teraz możemy zwizualizować dokładność zestawu ocen i utratę tych przebiegów.
import matplotlib.pyplot as plt
import seaborn as sns
def make_plot(data_frame):
plt.figure(figsize=(15, 5))
dff = data_frame.rename(
columns={'sparse_categorical_accuracy': 'Accuracy', 'loss': 'Loss'})
plt.subplot(121)
sns.lineplot(data=dff, x='Round', y='Accuracy', hue='NoiseMultiplier', palette='dark')
plt.subplot(122)
sns.lineplot(data=dff, x='Round', y='Loss', hue='NoiseMultiplier', palette='dark')
make_plot(data_frame)
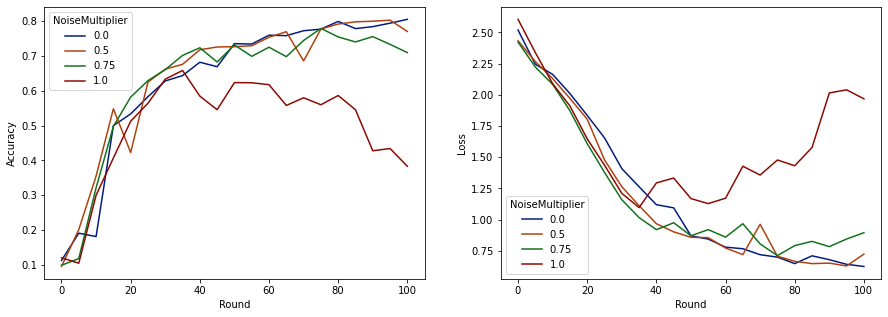
Wydaje się, że przy 50 oczekiwanych klientach na rundę model ten może tolerować mnożnik szumu do 0,5 bez pogorszenia jakości modelu. Mnożnik szumu równy 0,75 wydaje się powodować niewielką degradację modelu, a 1,0 powoduje rozbieżność modelu.
Zwykle istnieje kompromis między jakością modelu a prywatnością. Im wyższy poziom hałasu używamy, tym więcej prywatności możemy uzyskać przy takiej samej ilości czasu szkolenia i liczbie klientów. I odwrotnie, przy mniejszym hałasie możemy mieć dokładniejszy model, ale będziemy musieli trenować z większą liczbą klientów na rundę, aby osiągnąć docelowy poziom prywatności.
W powyższym eksperymencie możemy zdecydować, że niewielkie pogorszenie modelu na poziomie 0,75 jest akceptowalne w celu szybszego trenowania końcowego modelu, ale załóżmy, że chcemy dopasować wydajność modelu z mnożnikiem szumów 0,5.
Teraz możemy użyć funkcji tensorflow_privacy, aby określić, ilu oczekiwanych klientów na rundę potrzebujemy, aby uzyskać akceptowalną prywatność. Standardową praktyką jest wybieranie delty nieco mniejszej niż jeden w stosunku do liczby rekordów w zestawie danych. Ten zbiór danych ma łącznie 3383 użytkowników trenujących, więc skupmy się na (2, 1e-5)-DP.
Używamy prostego wyszukiwania binarnego według liczby klientów na rundę. Funkcja tensorflow_privacy używamy do oszacowania epsilon jest na podstawie Wang et al. (2018) i Mironowa i wsp. (2019) .
rdp_orders = ([1.25, 1.5, 1.75, 2., 2.25, 2.5, 3., 3.5, 4., 4.5] +
list(range(5, 64)) + [128, 256, 512])
total_clients = 3383
base_noise_multiplier = 0.5
base_clients_per_round = 50
target_delta = 1e-5
target_eps = 2
def get_epsilon(clients_per_round):
# If we use this number of clients per round and proportionally
# scale up the noise multiplier, what epsilon do we achieve?
q = clients_per_round / total_clients
noise_multiplier = base_noise_multiplier
noise_multiplier *= clients_per_round / base_clients_per_round
rdp = tfp.compute_rdp(
q, noise_multiplier=noise_multiplier, steps=rounds, orders=rdp_orders)
eps, _, _ = tfp.get_privacy_spent(rdp_orders, rdp, target_delta=target_delta)
return clients_per_round, eps, noise_multiplier
def find_needed_clients_per_round():
hi = get_epsilon(base_clients_per_round)
if hi[1] < target_eps:
return hi
# Grow interval exponentially until target_eps is exceeded.
while True:
lo = hi
hi = get_epsilon(2 * lo[0])
if hi[1] < target_eps:
break
# Binary search.
while hi[0] - lo[0] > 1:
mid = get_epsilon((lo[0] + hi[0]) // 2)
if mid[1] > target_eps:
lo = mid
else:
hi = mid
return hi
clients_per_round, _, noise_multiplier = find_needed_clients_per_round()
print(f'To get ({target_eps}, {target_delta})-DP, use {clients_per_round} '
f'clients with noise multiplier {noise_multiplier}.')
To get (2, 1e-05)-DP, use 120 clients with noise multiplier 1.2.
Teraz możemy trenować nasz ostateczny prywatny model do wydania.
rounds = 100
noise_multiplier = 1.2
clients_per_round = 120
data_frame = pd.DataFrame()
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
make_plot(data_frame)
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.08260678), ('loss', 2.6334999)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.1492212), ('loss', 2.259542)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.28847474), ('loss', 2.155699)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.3989518), ('loss', 2.0156953)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5086697), ('loss', 1.8261365)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.6204692), ('loss', 1.5602393)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.70008814), ('loss', 0.91155165)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.78421336), ('loss', 0.6820159)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7955525), ('loss', 0.6585961)])
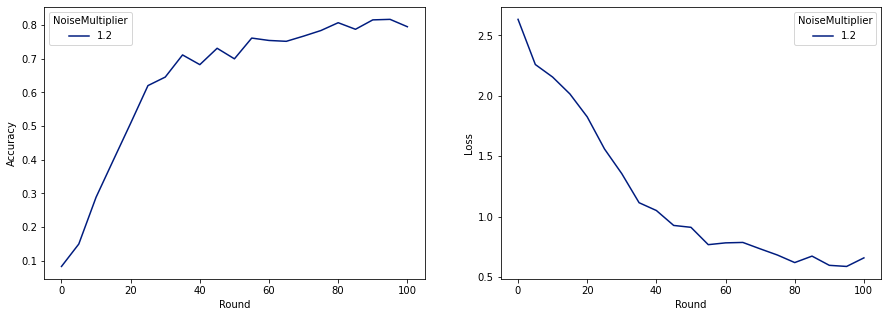
Jak widać, ostateczny model ma podobną stratę i dokładność do modelu wytrenowanego bez szumu, ale ten spełnia (2, 1e-5)-DP.
