 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza la fonte su GitHub Visualizza la fonte su GitHub |  Scarica taccuino Scarica taccuino |
Questa esercitazione dimostrerà le procedure consigliate per l'addestramento di modelli con privacy differenziale a livello di utente utilizzando Tensorflow Federated. Useremo l'algoritmo DP-SGD di Abadi et al., "Deep Learning con Privacy differenziale" modificato per a livello utente DP in un contesto federata in McMahan et al., "Modelli di apprendimento differenzialmente privato ricorrente della lingua" .
La privacy differenziale (DP) è un metodo ampiamente utilizzato per delimitare e quantificare la perdita di privacy dei dati sensibili durante l'esecuzione di attività di apprendimento. L'addestramento di un modello con DP a livello di utente garantisce che è improbabile che il modello impari qualcosa di significativo sui dati di qualsiasi individuo, ma può ancora (si spera!) apprendere modelli che esistono nei dati di molti clienti.
Addestreremo un modello sul set di dati EMNIST federato. Esiste un compromesso intrinseco tra utilità e privacy e può essere difficile addestrare un modello con un'elevata privacy che funzioni come un modello non privato all'avanguardia. Per convenienza in questo tutorial, ci alleneremo per soli 100 round, sacrificando un po' di qualità per dimostrare come allenarci con un'elevata privacy. Se usassimo più turni di addestramento, potremmo certamente avere un modello privato un po' più accurato, ma non così alto come un modello addestrato senza DP.
Prima di iniziare
Innanzitutto, assicuriamoci che il notebook sia connesso a un backend con i componenti pertinenti compilati.
!pip install --quiet --upgrade tensorflow_federated_nightly
!pip install --quiet --upgrade nest-asyncio
import nest_asyncio
nest_asyncio.apply()
Alcune importazioni di cui avremo bisogno per il tutorial. Useremo tensorflow_federated , il framework open-source per l'apprendimento della macchina e altri calcoli sui dati decentralizzati, così come tensorflow_privacy , la libreria open-source per l'implementazione e l'analisi di algoritmi in modo differenziale privati in tensorflow.
import collections
import numpy as np
import pandas as pd
import tensorflow as tf
import tensorflow_federated as tff
import tensorflow_privacy as tfp
Eseguire il seguente esempio "Hello World" per assicurarsi che l'ambiente TFF sia configurato correttamente. Se non funziona, si prega di fare riferimento alla installazione guida per le istruzioni.
@tff.federated_computation
def hello_world():
return 'Hello, World!'
hello_world()
b'Hello, World!'
Scarica e preelabora il set di dati EMNIST federato.
def get_emnist_dataset():
emnist_train, emnist_test = tff.simulation.datasets.emnist.load_data(
only_digits=True)
def element_fn(element):
return collections.OrderedDict(
x=tf.expand_dims(element['pixels'], -1), y=element['label'])
def preprocess_train_dataset(dataset):
# Use buffer_size same as the maximum client dataset size,
# 418 for Federated EMNIST
return (dataset.map(element_fn)
.shuffle(buffer_size=418)
.repeat(1)
.batch(32, drop_remainder=False))
def preprocess_test_dataset(dataset):
return dataset.map(element_fn).batch(128, drop_remainder=False)
emnist_train = emnist_train.preprocess(preprocess_train_dataset)
emnist_test = preprocess_test_dataset(
emnist_test.create_tf_dataset_from_all_clients())
return emnist_train, emnist_test
train_data, test_data = get_emnist_dataset()
Definisci il nostro modello.
def my_model_fn():
model = tf.keras.models.Sequential([
tf.keras.layers.Reshape(input_shape=(28, 28, 1), target_shape=(28 * 28,)),
tf.keras.layers.Dense(200, activation=tf.nn.relu),
tf.keras.layers.Dense(200, activation=tf.nn.relu),
tf.keras.layers.Dense(10)])
return tff.learning.from_keras_model(
keras_model=model,
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
input_spec=test_data.element_spec,
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()])
Determinare la sensibilità al rumore del modello.
Per ottenere garanzie DP a livello di utente, dobbiamo modificare l'algoritmo di media federata di base in due modi. Innanzitutto, gli aggiornamenti del modello dei client devono essere ritagliati prima della trasmissione al server, limitando l'influenza massima di qualsiasi client. In secondo luogo, il server deve aggiungere abbastanza rumore alla somma degli aggiornamenti dell'utente prima di calcolare la media per oscurare l'influenza del client nel caso peggiore.
Per ritaglio, usiamo il metodo di ritaglio adattivo di Andrew et al. 2021, differenzialmente Learning privato con Adaptive ritaglio , in modo da nessuna norma di ritaglio deve essere impostata in modo esplicito.
L'aggiunta di rumore in generale ridurrà l'utilità del modello, ma possiamo controllare la quantità di rumore nell'aggiornamento medio ad ogni turno con due manopole: la deviazione standard del rumore gaussiano aggiunto alla somma e il numero di client nel media. La nostra strategia sarà innanzitutto determinare quanto rumore può tollerare il modello con un numero relativamente piccolo di client per round con una perdita accettabile per l'utilità del modello. Quindi, per addestrare il modello finale, possiamo aumentare la quantità di rumore nella somma, aumentando proporzionalmente il numero di client per round (supponendo che il set di dati sia abbastanza grande da supportare quel numero di client per round). È improbabile che ciò influisca in modo significativo sulla qualità del modello, poiché l'unico effetto è ridurre la varianza dovuta al campionamento del cliente (infatti verificheremo che non lo faccia nel nostro caso).
A tal fine, formiamo prima una serie di modelli con 50 client per round, con quantità crescenti di rumore. Nello specifico, aumentiamo il "noise_multiplier" che è il rapporto tra la deviazione standard del rumore e la norma di clipping. Poiché utilizziamo il ritaglio adattivo, ciò significa che l'ampiezza effettiva del rumore cambia da tonda a tonda.
# Run five clients per thread. Increase this if your runtime is running out of
# memory. Decrease it if you have the resources and want to speed up execution.
tff.backends.native.set_local_python_execution_context(clients_per_thread=5)
total_clients = len(train_data.client_ids)
def train(rounds, noise_multiplier, clients_per_round, data_frame):
# Using the `dp_aggregator` here turns on differential privacy with adaptive
# clipping.
aggregation_factory = tff.learning.model_update_aggregator.dp_aggregator(
noise_multiplier, clients_per_round)
# We use Poisson subsampling which gives slightly tighter privacy guarantees
# compared to having a fixed number of clients per round. The actual number of
# clients per round is stochastic with mean clients_per_round.
sampling_prob = clients_per_round / total_clients
# Build a federated averaging process.
# Typically a non-adaptive server optimizer is used because the noise in the
# updates can cause the second moment accumulators to become very large
# prematurely.
learning_process = tff.learning.build_federated_averaging_process(
my_model_fn,
client_optimizer_fn=lambda: tf.keras.optimizers.SGD(0.01),
server_optimizer_fn=lambda: tf.keras.optimizers.SGD(1.0, momentum=0.9),
model_update_aggregation_factory=aggregation_factory)
eval_process = tff.learning.build_federated_evaluation(my_model_fn)
# Training loop.
state = learning_process.initialize()
for round in range(rounds):
if round % 5 == 0:
metrics = eval_process(state.model, [test_data])['eval']
if round < 25 or round % 25 == 0:
print(f'Round {round:3d}: {metrics}')
data_frame = data_frame.append({'Round': round,
'NoiseMultiplier': noise_multiplier,
**metrics}, ignore_index=True)
# Sample clients for a round. Note that if your dataset is large and
# sampling_prob is small, it would be faster to use gap sampling.
x = np.random.uniform(size=total_clients)
sampled_clients = [
train_data.client_ids[i] for i in range(total_clients)
if x[i] < sampling_prob]
sampled_train_data = [
train_data.create_tf_dataset_for_client(client)
for client in sampled_clients]
# Use selected clients for update.
state, metrics = learning_process.next(state, sampled_train_data)
metrics = eval_process(state.model, [test_data])['eval']
print(f'Round {rounds:3d}: {metrics}')
data_frame = data_frame.append({'Round': rounds,
'NoiseMultiplier': noise_multiplier,
**metrics}, ignore_index=True)
return data_frame
data_frame = pd.DataFrame()
rounds = 100
clients_per_round = 50
for noise_multiplier in [0.0, 0.5, 0.75, 1.0]:
print(f'Starting training with noise multiplier: {noise_multiplier}')
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
print()
Starting training with noise multiplier: 0.0
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.112289384), ('loss', 2.5190482)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.19075724), ('loss', 2.2449977)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.18115693), ('loss', 2.163907)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.49970612), ('loss', 2.01017)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5333317), ('loss', 1.8350543)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.5828517), ('loss', 1.6551636)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.7352077), ('loss', 0.8700141)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.7769152), ('loss', 0.6992781)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.8049814), ('loss', 0.62453026)])
Starting training with noise multiplier: 0.5
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.09526841), ('loss', 2.4332638)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.20128821), ('loss', 2.2664592)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.35472178), ('loss', 2.130336)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.5480995), ('loss', 1.9713942)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.42246276), ('loss', 1.8045483)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.624902), ('loss', 1.4785467)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.7265625), ('loss', 0.85801566)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.77720904), ('loss', 0.70615387)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7702537), ('loss', 0.72331005)])
Starting training with noise multiplier: 0.75
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.098672606), ('loss', 2.422002)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.11794671), ('loss', 2.2227976)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.3208513), ('loss', 2.083766)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.49752644), ('loss', 1.8728142)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5816761), ('loss', 1.6084186)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.62896746), ('loss', 1.378527)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.73153406), ('loss', 0.8705139)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.7789724), ('loss', 0.7113147)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.70944357), ('loss', 0.89495045)])
Starting training with noise multiplier: 1.0
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.12002841), ('loss', 2.60482)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.104574844), ('loss', 2.3388205)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.29966694), ('loss', 2.089262)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.4067398), ('loss', 1.9109797)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5123677), ('loss', 1.6472703)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.56416535), ('loss', 1.4362282)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.62323666), ('loss', 1.1682972)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.55968356), ('loss', 1.4779186)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.382837), ('loss', 1.9680436)])
Ora possiamo visualizzare l'accuratezza del set di valutazione e la perdita di tali esecuzioni.
import matplotlib.pyplot as plt
import seaborn as sns
def make_plot(data_frame):
plt.figure(figsize=(15, 5))
dff = data_frame.rename(
columns={'sparse_categorical_accuracy': 'Accuracy', 'loss': 'Loss'})
plt.subplot(121)
sns.lineplot(data=dff, x='Round', y='Accuracy', hue='NoiseMultiplier', palette='dark')
plt.subplot(122)
sns.lineplot(data=dff, x='Round', y='Loss', hue='NoiseMultiplier', palette='dark')
make_plot(data_frame)
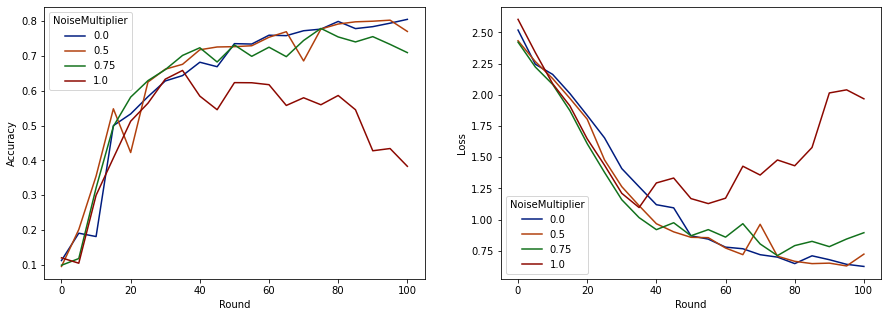
Sembra che con 50 client previsti per round, questo modello può tollerare un moltiplicatore di rumore fino a 0,5 senza degradare la qualità del modello. Un moltiplicatore di rumore di 0,75 sembra causare un po' di degrado del modello e 1,0 fa divergere il modello.
Di solito c'è un compromesso tra la qualità del modello e la privacy. Maggiore è il rumore che utilizziamo, maggiore è la privacy che possiamo ottenere per la stessa quantità di tempo di formazione e numero di client. Al contrario, con meno rumore, potremmo avere un modello più accurato, ma dovremo allenarci con più clienti per round per raggiungere il nostro livello di privacy target.
Con l'esperimento sopra, potremmo decidere che la piccola quantità di deterioramento del modello a 0,75 è accettabile per addestrare il modello finale più velocemente, ma supponiamo di voler abbinare le prestazioni del modello con moltiplicatore di rumore 0,5.
Ora possiamo usare le funzioni tensorflow_privacy per determinare quanti client attesi per round avremmo bisogno di ottenere una privacy accettabile. La pratica standard consiste nel scegliere un delta leggermente inferiore a uno rispetto al numero di record nel set di dati. Questo set di dati ha 3383 utenti di formazione totali, quindi puntiamo a (2, 1e-5)-DP.
Usiamo una semplice ricerca binaria sul numero di clienti per round. La funzione tensorflow_privacy che usiamo per valutare Epsilon si basa su Wang et al. (2018) e Mironov et al. (2019) .
rdp_orders = ([1.25, 1.5, 1.75, 2., 2.25, 2.5, 3., 3.5, 4., 4.5] +
list(range(5, 64)) + [128, 256, 512])
total_clients = 3383
base_noise_multiplier = 0.5
base_clients_per_round = 50
target_delta = 1e-5
target_eps = 2
def get_epsilon(clients_per_round):
# If we use this number of clients per round and proportionally
# scale up the noise multiplier, what epsilon do we achieve?
q = clients_per_round / total_clients
noise_multiplier = base_noise_multiplier
noise_multiplier *= clients_per_round / base_clients_per_round
rdp = tfp.compute_rdp(
q, noise_multiplier=noise_multiplier, steps=rounds, orders=rdp_orders)
eps, _, _ = tfp.get_privacy_spent(rdp_orders, rdp, target_delta=target_delta)
return clients_per_round, eps, noise_multiplier
def find_needed_clients_per_round():
hi = get_epsilon(base_clients_per_round)
if hi[1] < target_eps:
return hi
# Grow interval exponentially until target_eps is exceeded.
while True:
lo = hi
hi = get_epsilon(2 * lo[0])
if hi[1] < target_eps:
break
# Binary search.
while hi[0] - lo[0] > 1:
mid = get_epsilon((lo[0] + hi[0]) // 2)
if mid[1] > target_eps:
lo = mid
else:
hi = mid
return hi
clients_per_round, _, noise_multiplier = find_needed_clients_per_round()
print(f'To get ({target_eps}, {target_delta})-DP, use {clients_per_round} '
f'clients with noise multiplier {noise_multiplier}.')
To get (2, 1e-05)-DP, use 120 clients with noise multiplier 1.2.
Ora possiamo addestrare il nostro modello privato finale per il rilascio.
rounds = 100
noise_multiplier = 1.2
clients_per_round = 120
data_frame = pd.DataFrame()
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
make_plot(data_frame)
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.08260678), ('loss', 2.6334999)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.1492212), ('loss', 2.259542)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.28847474), ('loss', 2.155699)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.3989518), ('loss', 2.0156953)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5086697), ('loss', 1.8261365)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.6204692), ('loss', 1.5602393)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.70008814), ('loss', 0.91155165)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.78421336), ('loss', 0.6820159)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7955525), ('loss', 0.6585961)])
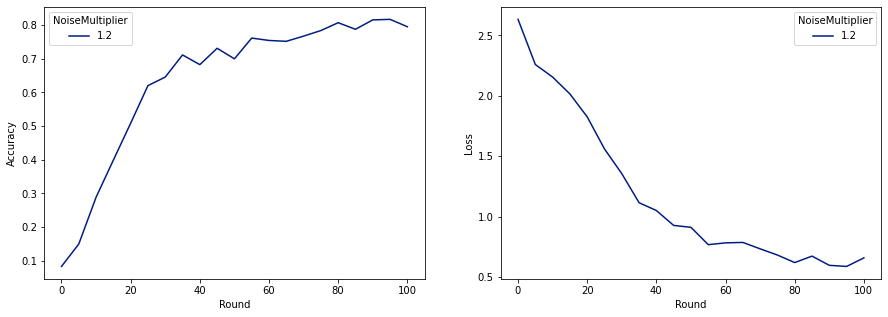
Come possiamo vedere, il modello finale ha una perdita e una precisione simili al modello addestrato senza rumore, ma questo soddisfa (2, 1e-5)-DP.
