 View on TensorFlow.org
|
 Run in Google Colab
|
 View on GitHub
|
 Download notebook
|
Welcome to the Learning to Rank Colab for TensorFlow Decision Forests (TF-DF). In this colab, you will learn how to use TF-DF for ranking.
This colab assumes you are familiar with the concepts presented the Beginner colab, notably about the installation about TF-DF.
In this colab, you will:
- Learn what a ranking model is.
- Train a Gradient Boosted Trees models on the LETOR3 dataset.
- Evaluate the quality of this model.
Installing TensorFlow Decision Forests
Install TF-DF by running the following cell.
pip install tensorflow_decision_forests
Wurlitzer is needed to display the detailed training logs in Colabs (when using verbose=2 in the model constructor).
pip install wurlitzer
Importing libraries
import os
# Keep using Keras 2
os.environ['TF_USE_LEGACY_KERAS'] = '1'
import tensorflow_decision_forests as tfdf
import numpy as np
import pandas as pd
import tensorflow as tf
import tf_keras
import math
The hidden code cell limits the output height in colab.
from IPython.core.magic import register_line_magic
from IPython.display import Javascript
from IPython.display import display as ipy_display
# Some of the model training logs can cover the full
# screen if not compressed to a smaller viewport.
# This magic allows setting a max height for a cell.
@register_line_magic
def set_cell_height(size):
ipy_display(
Javascript("google.colab.output.setIframeHeight(0, true, {maxHeight: " +
str(size) + "})"))
# Check the version of TensorFlow Decision Forests
print("Found TensorFlow Decision Forests v" + tfdf.__version__)
Found TensorFlow Decision Forests v1.9.0
What is a ranking model?
The goal of a ranking model is to correctly order items. For example, ranking can be used to select the best documents to retrieve following a user query.
A common way to represent a Ranking dataset is with a "relevance" score: The order of the elements is defined by their relevance: Items of greater relevance should be before lower relevance items. The cost of a mistake is defined by the difference between the relevance of the predicted item with the relevance of the correct item. For example, misordering two items with respective relevance 3 and 4 is not as bad as misordering two items with respective relevance 1 and 5.
TF-DF expects ranking datasets to be presented in a "flat" format. A dataset of queries and corresponding documents might look like this:
| query | document_id | feature_1 | feature_2 | relevance |
|---|---|---|---|---|
| cat | 1 | 0.1 | blue | 4 |
| cat | 2 | 0.5 | green | 1 |
| cat | 3 | 0.2 | red | 2 |
| dog | 4 | NA | red | 0 |
| dog | 5 | 0.2 | red | 0 |
| dog | 6 | 0.6 | green | 1 |
The relevance/label is a floating point numerical value between 0 and 5 (generally between 0 and 4) where 0 means "completely unrelated", 4 means "very relevant" and 5 means "same as the query".
In this example, Document 1 is very relevant to the query "cat", while document 2 is only "related" to cats. There are no documents is really talking about "dog" (the highest relevance is 1 for the document 6). However, the dog query is still expecting to return document 6 (since this is the document that talks the "most" about dogs).
Interestingly, decision forests are often good rankers, and many state-of-the-art ranking models are decision forests.
Let's train a Ranking model
In this example, use a sample of the
LETOR3
dataset. More precisely, we want to download the OHSUMED.zip from the LETOR3 repo. This dataset is stored in the
libsvm format, so we will need to convert it to csv.
archive_path = tf_keras.utils.get_file("letor.zip",
"https://download.microsoft.com/download/E/7/E/E7EABEF1-4C7B-4E31-ACE5-73927950ED5E/Letor.zip",
extract=True)
# Path to a ranking ataset using libsvm format.
raw_dataset_path = os.path.join(os.path.dirname(archive_path),"OHSUMED/Data/Fold1/trainingset.txt")
Downloading data from https://download.microsoft.com/download/E/7/E/E7EABEF1-4C7B-4E31-ACE5-73927950ED5E/Letor.zip 61824018/61824018 [==============================] - 7s 0us/step
Here are the first lines of the dataset:
head {raw_dataset_path}
The first step is to convert this dataset to the "flat" format mentioned above.
def convert_libsvm_to_csv(src_path, dst_path):
"""Converts a libsvm ranking dataset into a flat csv file.
Note: This code is specific to the LETOR3 dataset.
"""
dst_handle = open(dst_path, "w")
first_line = True
for src_line in open(src_path,"r"):
# Note: The last 3 items are comments.
items = src_line.split(" ")[:-3]
relevance = items[0]
group = items[1].split(":")[1]
features = [ item.split(":") for item in items[2:]]
if first_line:
# Csv header
dst_handle.write("relevance,group," + ",".join(["f_" + feature[0] for feature in features]) + "\n")
first_line = False
dst_handle.write(relevance + ",g_" + group + "," + (",".join([feature[1] for feature in features])) + "\n")
dst_handle.close()
# Convert the dataset.
csv_dataset_path="/tmp/ohsumed.csv"
convert_libsvm_to_csv(raw_dataset_path, csv_dataset_path)
# Load a dataset into a Pandas Dataframe.
dataset_df = pd.read_csv(csv_dataset_path)
# Display the first 3 examples.
dataset_df.head(3)
In this dataset, each row represents a pair of query/document (called "group"). The "relevance" tells how much the query matches the document.
The features of the query and the document are merged together in "f1-25". The exact definition of the features is not known, but it would be omething like:
- Number of words in queries
- Number of common words between the query and the document
- Cosinus similarity between an embedding of the query and an embedding of the document.
- ...
Let's convert the Pandas Dataframe into a TensorFlow Dataset:
dataset_ds = tfdf.keras.pd_dataframe_to_tf_dataset(dataset_df, label="relevance", task=tfdf.keras.Task.RANKING)
Let's configure and train our Ranking model.
%set_cell_height 400
model = tfdf.keras.GradientBoostedTreesModel(
task=tfdf.keras.Task.RANKING,
ranking_group="group",
num_trees=50)
model.fit(dataset_ds)
<IPython.core.display.Javascript object> Warning: The `num_threads` constructor argument is not set and the number of CPU is os.cpu_count()=32 > 32. Setting num_threads to 32. Set num_threads manually to use more than 32 cpus. WARNING:absl:The `num_threads` constructor argument is not set and the number of CPU is os.cpu_count()=32 > 32. Setting num_threads to 32. Set num_threads manually to use more than 32 cpus. Use /tmpfs/tmp/tmpzqjjgty3 as temporary training directory Reading training dataset... [WARNING 24-04-20 11:09:14.5069 UTC gradient_boosted_trees.cc:1840] "goss_alpha" set but "sampling_method" not equal to "GOSS". [WARNING 24-04-20 11:09:14.5069 UTC gradient_boosted_trees.cc:1851] "goss_beta" set but "sampling_method" not equal to "GOSS". [WARNING 24-04-20 11:09:14.5069 UTC gradient_boosted_trees.cc:1865] "selective_gradient_boosting_ratio" set but "sampling_method" not equal to "SELGB". Training dataset read in 0:00:03.986733. Found 9219 examples. Training model... Model trained in 0:00:00.757738 Compiling model... [INFO 24-04-20 11:09:19.2736 UTC kernel.cc:1233] Loading model from path /tmpfs/tmp/tmpzqjjgty3/model/ with prefix fa7585ffd7c24e56 [INFO 24-04-20 11:09:19.2748 UTC quick_scorer_extended.cc:911] The binary was compiled without AVX2 support, but your CPU supports it. Enable it for faster model inference. [INFO 24-04-20 11:09:19.2749 UTC abstract_model.cc:1344] Engine "GradientBoostedTreesQuickScorerExtended" built [INFO 24-04-20 11:09:19.2749 UTC kernel.cc:1061] Use fast generic engine Model compiled. <tf_keras.src.callbacks.History at 0x7fb6979cc8b0>
We can now look at the quality of the model on the validation dataset. By default, TF-DF trains ranking models to optimize the NDCG. The NDCG is a value between 0 and 1, where 1 is the perfect score. For this reason, -NDCG is the model loss.
import matplotlib.pyplot as plt
logs = model.make_inspector().training_logs()
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.plot([log.num_trees for log in logs], [log.evaluation.ndcg for log in logs])
plt.xlabel("Number of trees")
plt.ylabel("NDCG (validation)")
plt.subplot(1, 2, 2)
plt.plot([log.num_trees for log in logs], [log.evaluation.loss for log in logs])
plt.xlabel("Number of trees")
plt.ylabel("Loss (validation)")
plt.show()
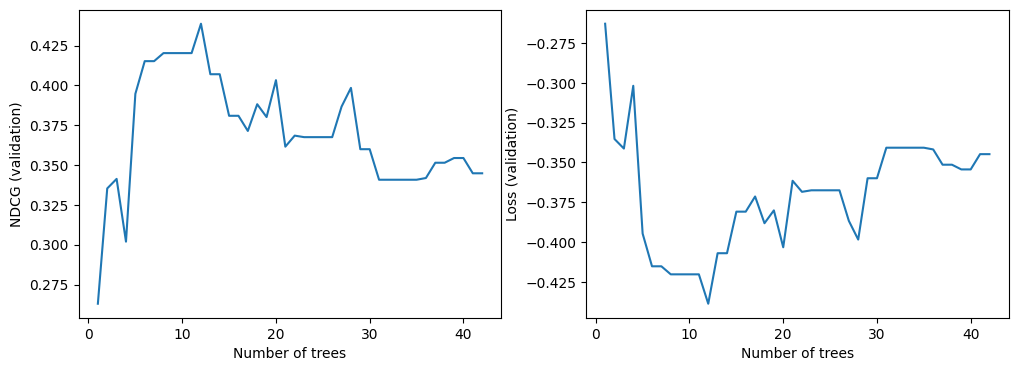
As for all TF-DF models, you can also look at the model report (Note: The model report also contains the training logs):
%set_cell_height 400
model.summary()
<IPython.core.display.Javascript object>
Model: "gradient_boosted_trees_model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
=================================================================
Total params: 1 (1.00 Byte)
Trainable params: 0 (0.00 Byte)
Non-trainable params: 1 (1.00 Byte)
_________________________________________________________________
Type: "GRADIENT_BOOSTED_TREES"
Task: RANKING
Label: "__LABEL"
Rank group: "group"
Input Features (25):
f_1
f_10
f_11
f_12
f_13
f_14
f_15
f_16
f_17
f_18
f_19
f_2
f_20
f_21
f_22
f_23
f_24
f_25
f_3
f_4
f_5
f_6
f_7
f_8
f_9
No weights
Variable Importance: INV_MEAN_MIN_DEPTH:
1. "f_9" 0.326164 ################
2. "f_3" 0.318071 ###############
3. "f_8" 0.308922 #############
4. "f_4" 0.271175 #########
5. "f_19" 0.221570 ###
6. "f_10" 0.215666 ##
7. "f_11" 0.206509 #
8. "f_22" 0.204742 #
9. "f_25" 0.204497 #
10. "f_23" 0.203238
11. "f_21" 0.200830
12. "f_24" 0.200445
13. "f_12" 0.198840
14. "f_18" 0.197676
15. "f_20" 0.196634
16. "f_6" 0.196085
17. "f_16" 0.196061
18. "f_2" 0.195683
19. "f_5" 0.195683
20. "f_13" 0.195559
21. "f_17" 0.195559
Variable Importance: NUM_AS_ROOT:
1. "f_3" 4.000000 ################
2. "f_4" 4.000000 ################
3. "f_8" 3.000000 ##########
4. "f_9" 1.000000
Variable Importance: NUM_NODES:
1. "f_8" 25.000000 ################
2. "f_19" 18.000000 ###########
3. "f_10" 15.000000 #########
4. "f_9" 14.000000 ########
5. "f_3" 13.000000 ########
6. "f_23" 7.000000 ####
7. "f_24" 6.000000 ###
8. "f_11" 5.000000 ##
9. "f_21" 5.000000 ##
10. "f_25" 5.000000 ##
11. "f_4" 5.000000 ##
12. "f_22" 4.000000 ##
13. "f_12" 3.000000 #
14. "f_20" 3.000000 #
15. "f_16" 2.000000
16. "f_6" 2.000000
17. "f_13" 1.000000
18. "f_17" 1.000000
19. "f_18" 1.000000
20. "f_2" 1.000000
21. "f_5" 1.000000
Variable Importance: SUM_SCORE:
1. "f_8" 10779.340861 ################
2. "f_9" 8831.772410 #############
3. "f_3" 4526.101184 ######
4. "f_4" 4360.245403 ######
5. "f_19" 2325.288894 ###
6. "f_10" 1881.848369 ##
7. "f_21" 1674.980191 ##
8. "f_11" 1127.632256 #
9. "f_23" 1021.834252 #
10. "f_24" 914.851512 #
11. "f_22" 885.619576 #
12. "f_25" 748.665007 #
13. "f_20" 310.610858
14. "f_16" 298.972842
15. "f_6" 212.376573
16. "f_12" 130.725240
17. "f_2" 112.124991
18. "f_18" 86.341193
19. "f_5" 65.103908
20. "f_13" 57.966947
21. "f_17" 21.930388
Loss: LAMBDA_MART_NDCG5
Validation loss value: -0.438692
Number of trees per iteration: 1
Node format: NOT_SET
Number of trees: 12
Total number of nodes: 286
Number of nodes by tree:
Count: 12 Average: 23.8333 StdDev: 3.50793
Min: 17 Max: 29 Ignored: 0
----------------------------------------------
[ 17, 18) 1 8.33% 8.33% ###
[ 18, 19) 0 0.00% 8.33%
[ 19, 20) 1 8.33% 16.67% ###
[ 20, 21) 0 0.00% 16.67%
[ 21, 22) 2 16.67% 33.33% #######
[ 22, 23) 0 0.00% 33.33%
[ 23, 24) 1 8.33% 41.67% ###
[ 24, 25) 0 0.00% 41.67%
[ 25, 26) 3 25.00% 66.67% ##########
[ 26, 27) 0 0.00% 66.67%
[ 27, 28) 3 25.00% 91.67% ##########
[ 28, 29) 0 0.00% 91.67%
[ 29, 29] 1 8.33% 100.00% ###
Depth by leafs:
Count: 149 Average: 4.14094 StdDev: 1.08696
Min: 1 Max: 5 Ignored: 0
----------------------------------------------
[ 1, 2) 2 1.34% 1.34%
[ 2, 3) 18 12.08% 13.42% ##
[ 3, 4) 13 8.72% 22.15% ##
[ 4, 5) 40 26.85% 48.99% #####
[ 5, 5] 76 51.01% 100.00% ##########
Number of training obs by leaf:
Count: 149 Average: 673.691 StdDev: 2015.44
Min: 5 Max: 8211 Ignored: 0
----------------------------------------------
[ 5, 415) 127 85.23% 85.23% ##########
[ 415, 825) 6 4.03% 89.26%
[ 825, 1236) 2 1.34% 90.60%
[ 1236, 1646) 0 0.00% 90.60%
[ 1646, 2056) 0 0.00% 90.60%
[ 2056, 2467) 1 0.67% 91.28%
[ 2467, 2877) 0 0.00% 91.28%
[ 2877, 3287) 0 0.00% 91.28%
[ 3287, 3698) 1 0.67% 91.95%
[ 3698, 4108) 0 0.00% 91.95%
[ 4108, 4518) 0 0.00% 91.95%
[ 4518, 4929) 1 0.67% 92.62%
[ 4929, 5339) 0 0.00% 92.62%
[ 5339, 5749) 0 0.00% 92.62%
[ 5749, 6160) 1 0.67% 93.29%
[ 6160, 6570) 0 0.00% 93.29%
[ 6570, 6980) 0 0.00% 93.29%
[ 6980, 7391) 0 0.00% 93.29%
[ 7391, 7801) 8 5.37% 98.66% #
[ 7801, 8211] 2 1.34% 100.00%
Attribute in nodes:
25 : f_8 [NUMERICAL]
18 : f_19 [NUMERICAL]
15 : f_10 [NUMERICAL]
14 : f_9 [NUMERICAL]
13 : f_3 [NUMERICAL]
7 : f_23 [NUMERICAL]
6 : f_24 [NUMERICAL]
5 : f_4 [NUMERICAL]
5 : f_25 [NUMERICAL]
5 : f_21 [NUMERICAL]
5 : f_11 [NUMERICAL]
4 : f_22 [NUMERICAL]
3 : f_20 [NUMERICAL]
3 : f_12 [NUMERICAL]
2 : f_6 [NUMERICAL]
2 : f_16 [NUMERICAL]
1 : f_5 [NUMERICAL]
1 : f_2 [NUMERICAL]
1 : f_18 [NUMERICAL]
1 : f_17 [NUMERICAL]
1 : f_13 [NUMERICAL]
Attribute in nodes with depth <= 0:
4 : f_4 [NUMERICAL]
4 : f_3 [NUMERICAL]
3 : f_8 [NUMERICAL]
1 : f_9 [NUMERICAL]
Attribute in nodes with depth <= 1:
11 : f_9 [NUMERICAL]
9 : f_8 [NUMERICAL]
4 : f_4 [NUMERICAL]
4 : f_3 [NUMERICAL]
1 : f_25 [NUMERICAL]
1 : f_24 [NUMERICAL]
1 : f_23 [NUMERICAL]
1 : f_22 [NUMERICAL]
1 : f_19 [NUMERICAL]
1 : f_11 [NUMERICAL]
Attribute in nodes with depth <= 2:
15 : f_8 [NUMERICAL]
12 : f_9 [NUMERICAL]
11 : f_3 [NUMERICAL]
6 : f_19 [NUMERICAL]
5 : f_4 [NUMERICAL]
2 : f_25 [NUMERICAL]
2 : f_11 [NUMERICAL]
2 : f_10 [NUMERICAL]
1 : f_24 [NUMERICAL]
1 : f_23 [NUMERICAL]
1 : f_22 [NUMERICAL]
1 : f_18 [NUMERICAL]
1 : f_17 [NUMERICAL]
Attribute in nodes with depth <= 3:
22 : f_8 [NUMERICAL]
13 : f_9 [NUMERICAL]
11 : f_3 [NUMERICAL]
10 : f_19 [NUMERICAL]
9 : f_10 [NUMERICAL]
5 : f_4 [NUMERICAL]
5 : f_23 [NUMERICAL]
5 : f_11 [NUMERICAL]
4 : f_25 [NUMERICAL]
4 : f_22 [NUMERICAL]
4 : f_21 [NUMERICAL]
3 : f_24 [NUMERICAL]
2 : f_12 [NUMERICAL]
1 : f_18 [NUMERICAL]
1 : f_17 [NUMERICAL]
Attribute in nodes with depth <= 5:
25 : f_8 [NUMERICAL]
18 : f_19 [NUMERICAL]
15 : f_10 [NUMERICAL]
14 : f_9 [NUMERICAL]
13 : f_3 [NUMERICAL]
7 : f_23 [NUMERICAL]
6 : f_24 [NUMERICAL]
5 : f_4 [NUMERICAL]
5 : f_25 [NUMERICAL]
5 : f_21 [NUMERICAL]
5 : f_11 [NUMERICAL]
4 : f_22 [NUMERICAL]
3 : f_20 [NUMERICAL]
3 : f_12 [NUMERICAL]
2 : f_6 [NUMERICAL]
2 : f_16 [NUMERICAL]
1 : f_5 [NUMERICAL]
1 : f_2 [NUMERICAL]
1 : f_18 [NUMERICAL]
1 : f_17 [NUMERICAL]
1 : f_13 [NUMERICAL]
Condition type in nodes:
137 : HigherCondition
Condition type in nodes with depth <= 0:
12 : HigherCondition
Condition type in nodes with depth <= 1:
34 : HigherCondition
Condition type in nodes with depth <= 2:
60 : HigherCondition
Condition type in nodes with depth <= 3:
99 : HigherCondition
Condition type in nodes with depth <= 5:
137 : HigherCondition
Training logs:
Number of iteration to final model: 12
Iter:1 train-loss:-0.346669 valid-loss:-0.262935 train-NDCG@5:0.346669 valid-NDCG@5:0.262935
Iter:2 train-loss:-0.412635 valid-loss:-0.335301 train-NDCG@5:0.412635 valid-NDCG@5:0.335301
Iter:3 train-loss:-0.468270 valid-loss:-0.341295 train-NDCG@5:0.468270 valid-NDCG@5:0.341295
Iter:4 train-loss:-0.481511 valid-loss:-0.301897 train-NDCG@5:0.481511 valid-NDCG@5:0.301897
Iter:5 train-loss:-0.473165 valid-loss:-0.394670 train-NDCG@5:0.473165 valid-NDCG@5:0.394670
Iter:6 train-loss:-0.496260 valid-loss:-0.415201 train-NDCG@5:0.496260 valid-NDCG@5:0.415201
Iter:16 train-loss:-0.526791 valid-loss:-0.380900 train-NDCG@5:0.526791 valid-NDCG@5:0.380900
Iter:26 train-loss:-0.560398 valid-loss:-0.367496 train-NDCG@5:0.560398 valid-NDCG@5:0.367496
Iter:36 train-loss:-0.584252 valid-loss:-0.341845 train-NDCG@5:0.584252 valid-NDCG@5:0.341845
And if you are curious, you can also plot the model:
tfdf.model_plotter.plot_model_in_colab(model, tree_idx=0, max_depth=3)
Predicting with a ranking model
For an incoming query, we can use our ranking model to predict the relevance of a stack of documents. In practice this means that for each query, we must come up with a set of documents that may or may not be relevant to the query. We call these documents our candidate documents. For each pair query/candidate document, we can compute the same features used during training. This is our serving dataset.
Going back to the example from the beginning of this tutorial, the serving dataset might look like this:
| query | document_id | feature_1 | feature_2 |
|---|---|---|---|
| fish | 32 | 0.3 | blue |
| fish | 33 | 1.0 | green |
| fish | 34 | 0.4 | blue |
| fish | 35 | NA | brown |
Observe that relevance is not part of the serving dataset, since this is what the model is trying to predict.
The serving dataset is fed to the TF-DF model and assigns a relevance score to each document.
| query | document_id | feature_1 | feature_2 | relevance |
|---|---|---|---|---|
| fish | 32 | 0.3 | blue | 0.325 |
| fish | 33 | 1.0 | green | 0.125 |
| fish | 34 | 0.4 | blue | 0.155 |
| fish | 35 | NA | brown | 0.593 |
This means that the document with document_id 35 is predicted to be most relevant for query "fish".
Let's try to do this with our real model.
# Path to a test dataset using libsvm format.
test_dataset_path = os.path.join(os.path.dirname(archive_path),"OHSUMED/Data/Fold1/testset.txt")
# Convert the dataset.
csv_test_dataset_path="/tmp/ohsumed_test.csv"
convert_libsvm_to_csv(raw_dataset_path, csv_test_dataset_path)
# Load a dataset into a Pandas Dataframe.
test_dataset_df = pd.read_csv(csv_test_dataset_path)
# Display the first 3 examples.
test_dataset_df.head(3)
Suppose our query is "g_5" and the test dataset already contains the candidate documents for this query.
# Filter by "g_5"
serving_dataset_df = test_dataset_df[test_dataset_df['group'] == 'g_5']
# Remove the columns for group and relevance, not needed for predictions.
serving_dataset_df = serving_dataset_df.drop(['relevance', 'group'], axis=1)
# Convert to a Tensorflow dataset
serving_dataset_ds = tfdf.keras.pd_dataframe_to_tf_dataset(serving_dataset_df, task=tfdf.keras.Task.RANKING)
# Run predictions with on all candidate documents
predictions = model.predict(serving_dataset_ds)
1/1 [==============================] - 0s 176ms/step
We can use add the predictions to the dataframe and use them to find the documents with the highest scores.
serving_dataset_df['prediction_score'] = predictions
serving_dataset_df.sort_values(by=['prediction_score'], ascending=False).head()