s3_o4_d

  • Mô tả :

Bộ dữ liệu được mô tả lần đầu trong phần "Đối tượng 3D của Stanford" trong bài báo Disentangleling by Subspace Diffusion . Dữ liệu bao gồm 100.000 kết xuất của mỗi đối tượng Thỏ và Rồng từ Kho lưu trữ Quét 3D của Stanford . Nhiều đối tượng có thể được thêm vào trong tương lai, nhưng chỉ có Thỏ và Rồng được sử dụng trong bài báo. Mỗi đối tượng được hiển thị với ánh sáng được lấy mẫu đồng nhất từ ​​một điểm trên 2 hình cầu và xoay 3D được lấy mẫu đồng nhất. Các trạng thái tiềm ẩn thực sự được cung cấp dưới dạng mảng NumPy cùng với hình ảnh. Ánh sáng được cung cấp dưới dạng 3 vectơ với định mức đơn vị, trong khi phép quay được cung cấp dưới dạng ma trận bậc bốn và ma trận trực giao 3x3.

Có nhiều điểm tương đồng giữa S3O4D và bộ dữ liệu điểm chuẩn ML hiện có như NORB , Ghế 3D , Hình dạng 3D và nhiều thứ khác, cũng bao gồm kết xuất của một tập hợp đối tượng trong các điều kiện chiếu sáng và tư thế khác nhau. Tuy nhiên, không có bộ dữ liệu nào trong số các bộ dữ liệu hiện có này bao gồm đầy đủ các phép quay trong 3D - hầu hết chỉ bao gồm một tập hợp con các thay đổi đối với độ cao và góc phương vị. Hình ảnh S3O4D được lấy mẫu thống nhất và độc lập với toàn bộ không gian xoay và chiếu sáng, nghĩa là tập dữ liệu chứa các đối tượng lộn ngược và được chiếu sáng từ phía sau hoặc bên dưới. Chúng tôi tin rằng điều này làm cho S3O4D đặc biệt phù hợp cho nghiên cứu về các mô hình tổng quát trong đó không gian tiềm ẩn có cấu trúc liên kết không tầm thường, cũng như cho các phương pháp học đa tạp chung trong đó độ cong của đa tạp là quan trọng.

Tách ra ví dụ
'bunny_test' 20.000
'bunny_train' 80.000
'dragon_test' 20.000
'dragon_train' 80.000
  • Tính năng :
FeaturesDict({
    'illumination': Tensor(shape=(3,), dtype=tf.float32),
    'image': Image(shape=(256, 256, 3), dtype=tf.uint8),
    'label': ClassLabel(shape=(), dtype=tf.int64, num_classes=2),
    'pose_mat': Tensor(shape=(3, 3), dtype=tf.float32),
    'pose_quat': Tensor(shape=(4,), dtype=tf.float32),
})

@article{pfau2020disentangling,
  title={Disentangling by Subspace Diffusion},
  author={Pfau, David and Higgins, Irina and Botev, Aleksandar and Racani\`ere,
  S{\'e}bastian},
  journal={Advances in Neural Information Processing Systems (NeurIPS)},
  year={2020}
}

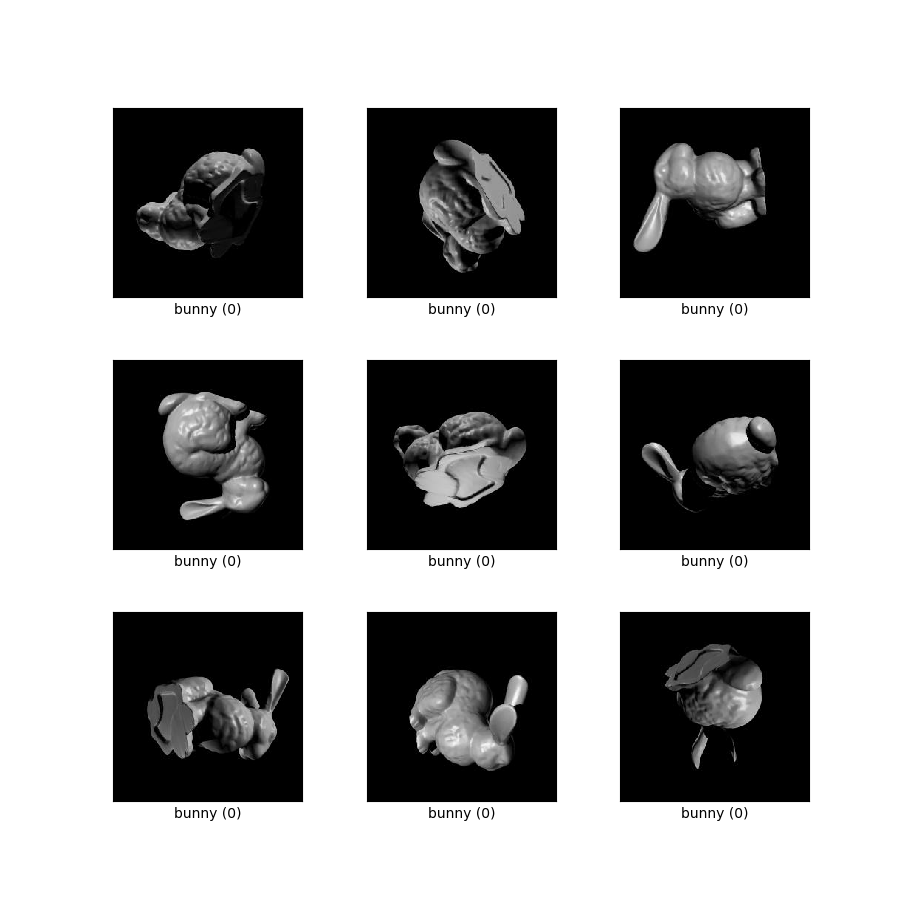
Hình dung