- Descrição :
O conjunto de dados descrito pela primeira vez na seção "Stanford 3D Objects" do artigo Disentangling by Subspace Diffusion . Os dados consistem em 100.000 renderizações de cada um dos objetos Bunny e Dragon do Stanford 3D Scanning Repository . Mais objetos podem ser adicionados no futuro, mas apenas o Coelhinho e o Dragão são usados no papel. Cada objeto é renderizado com uma iluminação amostrada uniformemente de um ponto na esfera 2 e uma rotação 3D amostrada uniformemente. Os verdadeiros estados latentes são fornecidos como matrizes NumPy junto com as imagens. A iluminação é dada como um 3-vetor com norma unitária, enquanto a rotação é fornecida como um quatérnio e uma matriz ortogonal 3x3.
Existem muitas semelhanças entre o S3O4D e os conjuntos de dados de referência de ML existentes, como NORB , 3D Chairs , 3D Shapes e muitos outros, que também incluem renderizações de um conjunto de objetos sob diferentes poses e condições de iluminação. No entanto, nenhum desses conjuntos de dados existentes inclui a variedade completa de rotações em 3D - a maioria inclui apenas um subconjunto de alterações de elevação e azimute. As imagens S3O4D são amostradas de maneira uniforme e independente do espaço total de rotações e iluminações, o que significa que o conjunto de dados contém objetos que estão de cabeça para baixo e iluminados por trás ou por baixo. Acreditamos que isso torna o S3O4D adequado exclusivamente para pesquisa em modelos generativos onde o espaço latente tem topologia não trivial, bem como para métodos de aprendizado de variedades gerais onde a curvatura da variedade é importante.
Página inicial : https://github.com/deepmind/deepmind-research/tree/master/geomancer#stanford-3d-objects-for-disentangling-s3o4d
Código -fonte:
tfds.image.s3o4d.S3O4DVersões :
-
1.0.0(padrão): versão inicial.
-
Tamanho do download :
911.68 MiBTamanho do conjunto de dados :
1.01 GiBArmazenado em cache automaticamente ( documentação ): Não
Divisões :
| Dividir | Exemplos |
|---|---|
'bunny_test' | 20.000 |
'bunny_train' | 80.000 |
'dragon_test' | 20.000 |
'dragon_train' | 80.000 |
- Características :
FeaturesDict({
'illumination': Tensor(shape=(3,), dtype=tf.float32),
'image': Image(shape=(256, 256, 3), dtype=tf.uint8),
'label': ClassLabel(shape=(), dtype=tf.int64, num_classes=2),
'pose_mat': Tensor(shape=(3, 3), dtype=tf.float32),
'pose_quat': Tensor(shape=(4,), dtype=tf.float32),
})
Chaves supervisionadas (Consulte
as_superviseddoc ):NoneCitação :
@article{pfau2020disentangling,
title={Disentangling by Subspace Diffusion},
author={Pfau, David and Higgins, Irina and Botev, Aleksandar and Racani\`ere,
S{\'e}bastian},
journal={Advances in Neural Information Processing Systems (NeurIPS)},
year={2020}
}
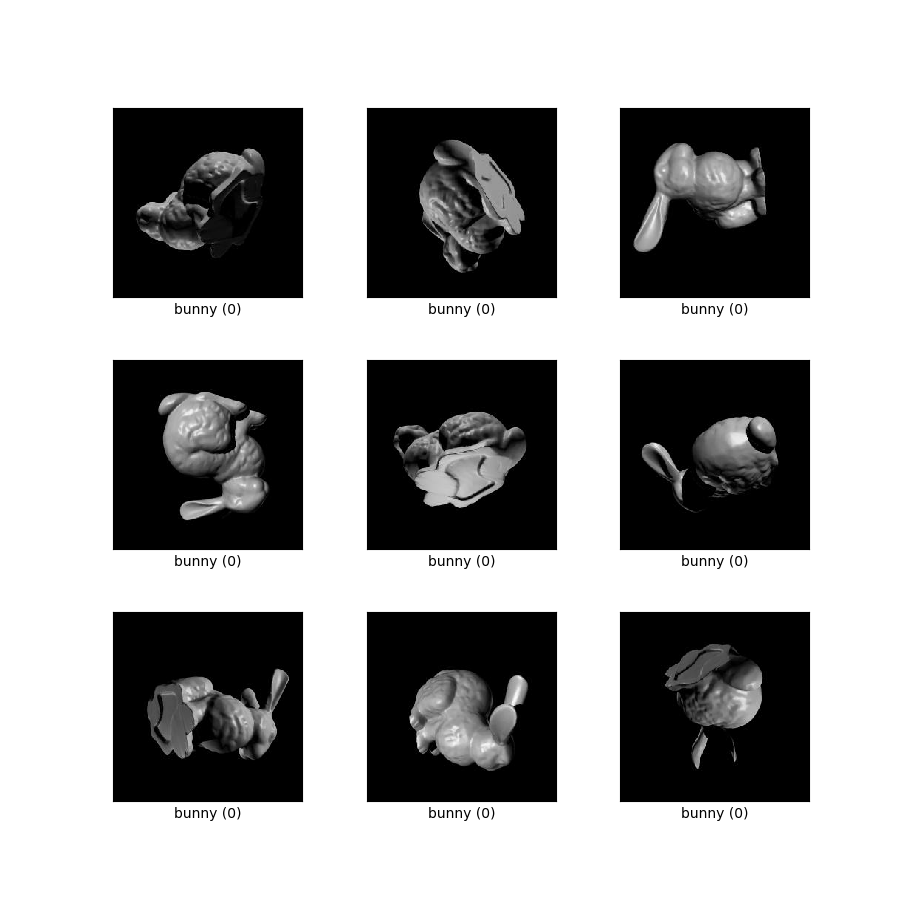
- Figura ( tfds.show_examples ):
- Exemplos ( tfds.as_dataframe ):

