s3_o4_d

  • Descriptif :

L'ensemble de données décrit pour la première fois dans la section "Stanford 3D Objects" de l'article Disentangling by Subspace Diffusion . Les données consistent en 100 000 rendus de chacun des objets Bunny et Dragon du Stanford 3D Scanning Repository . Plus d'objets peuvent être ajoutés à l'avenir, mais seuls le lapin et le dragon sont utilisés dans le document. Chaque objet est rendu avec un éclairage uniformément échantillonné à partir d'un point sur la sphère 2 et une rotation 3D uniformément échantillonnée. Les véritables états latents sont fournis sous forme de tableaux NumPy avec les images. L'éclairage est donné sous la forme d'un vecteur 3 avec une norme unitaire, tandis que la rotation est fournie à la fois sous la forme d'un quaternion et d'une matrice orthogonale 3x3.

Il existe de nombreuses similitudes entre S3O4D et les ensembles de données de référence ML existants tels que NORB , 3D Chairs , 3D Shapes et bien d'autres, qui incluent également des rendus d'un ensemble d'objets sous différentes conditions de pose et d'éclairage. Cependant, aucun de ces ensembles de données existants n'inclut la variété complète des rotations en 3D - la plupart n'incluent qu'un sous-ensemble de changements d'élévation et d'azimut. Les images S3O4D sont échantillonnées uniformément et indépendamment de l'espace complet des rotations et des illuminations, ce qui signifie que l'ensemble de données contient des objets qui sont à l'envers et éclairés par derrière ou par dessous. Nous pensons que cela rend S3O4D particulièrement adapté à la recherche sur les modèles génératifs où l'espace latent a une topologie non triviale, ainsi qu'aux méthodes générales d'apprentissage de la variété où la courbure de la variété est importante.

Diviser Exemples
'bunny_test' 20 000
'bunny_train' 80 000
'dragon_test' 20 000
'dragon_train' 80 000
  • Caractéristiques :
FeaturesDict({
    'illumination': Tensor(shape=(3,), dtype=tf.float32),
    'image': Image(shape=(256, 256, 3), dtype=tf.uint8),
    'label': ClassLabel(shape=(), dtype=tf.int64, num_classes=2),
    'pose_mat': Tensor(shape=(3, 3), dtype=tf.float32),
    'pose_quat': Tensor(shape=(4,), dtype=tf.float32),
})

@article{pfau2020disentangling,
  title={Disentangling by Subspace Diffusion},
  author={Pfau, David and Higgins, Irina and Botev, Aleksandar and Racani\`ere,
  S{\'e}bastian},
  journal={Advances in Neural Information Processing Systems (NeurIPS)},
  year={2020}
}

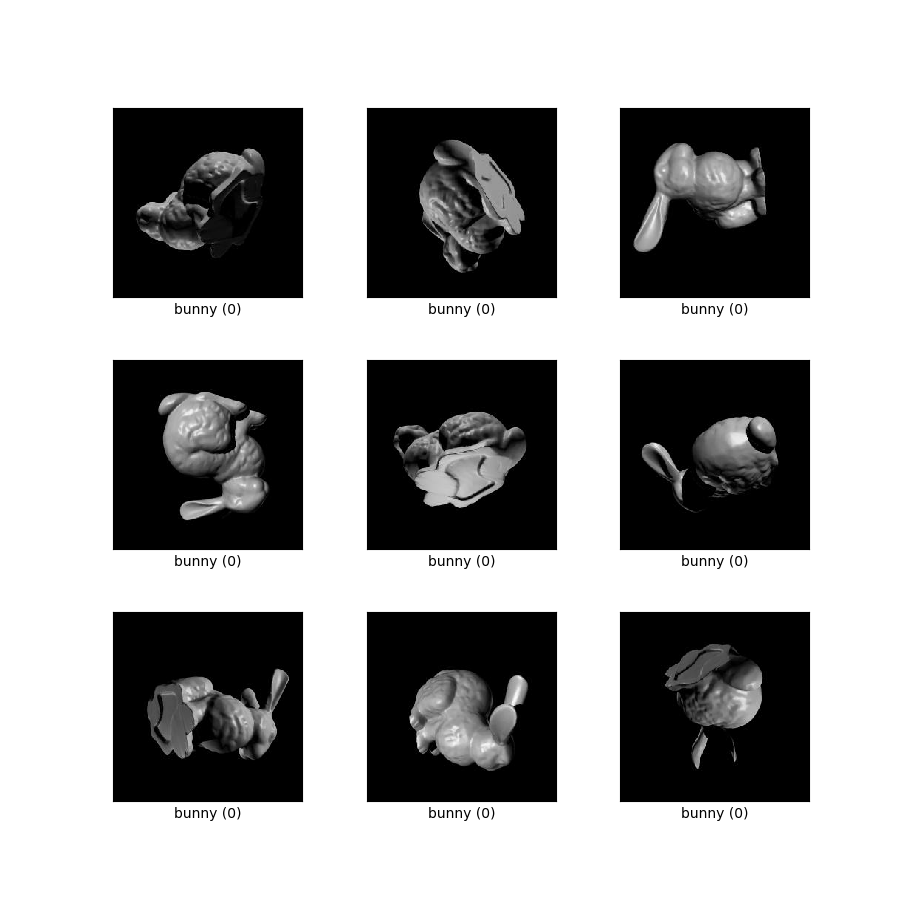
Visualisation