Bản quyền 2021 Các tác giả TF-Agents.
 Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
Giới thiệu
Học tập củng cố (RL) là một khuôn khổ chung trong đó các đại lý học cách thực hiện các hành động trong một môi trường để tối đa hóa phần thưởng. Hai thành phần chính là môi trường, đại diện cho vấn đề cần giải quyết và tác nhân, đại diện cho thuật toán học.
Tác nhân và môi trường liên tục tương tác với nhau. Tại mỗi bước thời gian, các đại lý có một hành động đối với môi trường dựa trên chính sách của nó \(\pi(a_t|s_t)\), nơi \(s_t\) là quan sát hiện từ môi trường, và nhận được một phần thưởng \(r_{t+1}\) và quan sát tiếp theo \(s_{t+1}\) từ môi trường . Mục tiêu là cải thiện chính sách để tối đa hóa tổng phần thưởng (lợi nhuận).
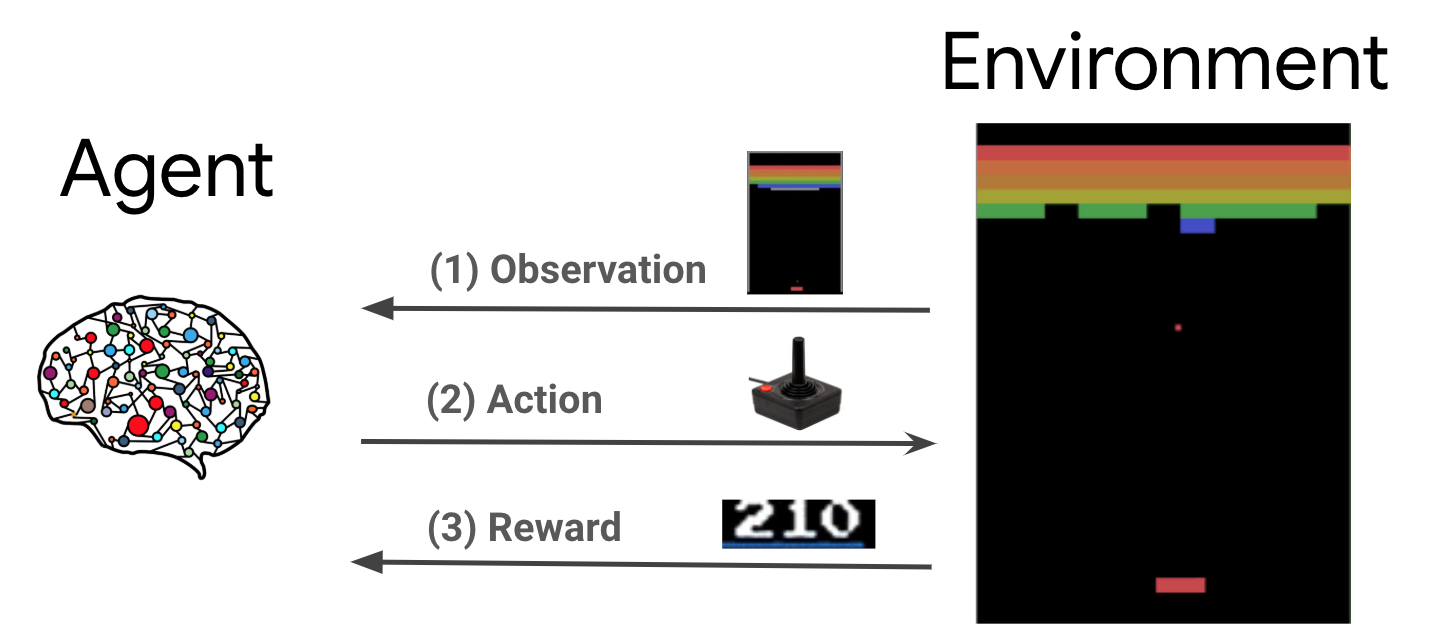
Đây là một khuôn khổ rất chung và có thể mô hình hóa nhiều vấn đề ra quyết định tuần tự như trò chơi, người máy, v.v.
Môi trường Cartpole
Môi trường Cartpole là một trong những vấn đề học tăng cường cổ điển nổi tiếng nhất ( "Hello, World!" Của RL). Một chiếc sào được gắn vào xe đẩy, có thể di chuyển dọc theo đường ray không ma sát. Trụ bắt đầu thẳng đứng và mục đích là ngăn không cho nó đổ bằng cách điều khiển xe đẩy.
- Các quan sát từ môi trường \(s_t\) là một vector 4D đại diện cho vị trí và vận tốc của giỏ hàng, và các góc độ và vận tốc góc của cực.
- Các đại lý có thể kiểm soát hệ thống bằng cách thực hiện một trong 2 hành động \(a_t\): đẩy giỏ hàng đúng (+1) hoặc trái (-1).
- Một phần thưởng \(r_{t+1} = 1\) được cung cấp cho mỗi bước thời gian mà cực vẫn thẳng đứng. Tập kết thúc khi một trong những điều sau là đúng:
- đầu cực vượt qua một số giới hạn góc
- xe đẩy di chuyển ra ngoài rìa thế giới
- 200 bước thời gian trôi qua.
Mục tiêu của đại lý là để học hỏi một chính sách \(\pi(a_t|s_t)\) để tối đa hóa tổng phần thưởng trong một tập \(\sum_{t=0}^{T} \gamma^t r_t\). Dưới đây \(\gamma\) là một yếu tố giảm giá trong \([0, 1]\) rằng giảm giá trong tương lai phần thưởng tương ứng với phần thưởng ngay lập tức. Thông số này giúp chúng tôi tập trung chính sách, khiến chính sách quan tâm hơn đến việc nhanh chóng nhận được phần thưởng.
Đại lý DQN
Các DQN (Sâu Q-Network) thuật toán được phát triển bởi DeepMind trong năm 2015. Nó đã có thể giải quyết một loạt các trò chơi Atari (một số mức siêu nhân) bằng cách kết hợp học tăng cường và mạng lưới thần kinh sâu theo tỷ lệ. Các thuật toán được phát triển bằng cách tăng cường một thuật toán RL cổ điển được gọi là Q-Learning với các mạng thần kinh sâu và một kỹ thuật gọi là kinh nghiệm phát lại.
Q-Learning
Q-Learning dựa trên khái niệm về hàm Q. Q-function (aka hàm giá trị trạng thái hành động) của một chính sách \(\pi\), \(Q^{\pi}(s, a)\), các biện pháp lợi nhuận kỳ vọng hoặc tiền chiết khấu của phần thưởng thu được từ nhà nước \(s\) bằng cách tham gia hành động \(a\) đầu tiên và sau chính sách \(\pi\) sau đó. Chúng tôi xác định tối ưu Q-chức năng \(Q^*(s, a)\) như sự trở lại tối đa có thể đạt được bắt đầu từ sự quan sát \(s\), hành động \(a\) và theo đuổi chính sách tối ưu sau đó. Tối ưu Q-chức năng tuân theo phương trình tối ưu Bellman sau:
\(\begin{equation}Q^\ast(s, a) = \mathbb{E}[ r + \gamma \max_{a'} Q^\ast(s', a') ]\end{equation}\)
Điều này có nghĩa rằng sự trở lại tối đa từ nhà nước \(s\) và hành động \(a\) là tổng các phần thưởng ngay lập tức \(r\) và sự trở lại (chiết khấu bởi \(\gamma\)) thu được bằng cách làm theo các chính sách tối ưu sau đó cho đến khi kết thúc các tập phim ( tức là, phần thưởng tối đa từ trạng thái tiếp theo \(s'\)). Kỳ vọng được tính cả trên việc phân phối các phần thưởng ngay lập tức \(r\) và các quốc gia tiếp theo có thể \(s'\).
Ý tưởng cơ bản đằng sau Q-Learning là sử dụng phương trình tối ưu Bellman như một bản cập nhật lặp \(Q_{i+1}(s, a) \leftarrow \mathbb{E}\left[ r + \gamma \max_{a'} Q_{i}(s', a')\right]\), và nó có thể được hiển thị mà hội tụ này để tối ưu \(Q\)-function, tức là \(Q_i \rightarrow Q^*\) như \(i \rightarrow \infty\) (xem DQN giấy ).
Học hỏi sâu
Đối với hầu hết các vấn đề, đó là không thực tế để đại diện cho \(Q\)-function như một bảng chứa giá trị cho mỗi sự kết hợp của \(s\) và \(a\). Thay vào đó, chúng tôi đào tạo một hàm approximator, chẳng hạn như một mạng lưới thần kinh với các thông số \(\theta\), để ước tính Q-giá trị, tức là \(Q(s, a; \theta) \approx Q^*(s, a)\). Điều này có thể thực hiện bằng cách giảm thiểu sự mất mát sau đối với mỗi bước \(i\):
\(\begin{equation}L_i(\theta_i) = \mathbb{E}_{s, a, r, s'\sim \rho(.)} \left[ (y_i - Q(s, a; \theta_i))^2 \right]\end{equation}\) nơi \(y_i = r + \gamma \max_{a'} Q(s', a'; \theta_{i-1})\)
Ở đây, \(y_i\) được gọi là mục tiêu TD (chênh lệch thời gian), và \(y_i - Q\) được gọi là lỗi TD. \(\rho\) đại diện phân phối của hành vi, phân phối qua chuyển \(\{s, a, r, s'\}\) thu thập từ môi trường.
Lưu ý rằng các thông số từ phiên trước \(\theta_{i-1}\) là cố định và không được cập nhật. Trong thực tế, chúng tôi sử dụng ảnh chụp nhanh các tham số mạng từ một vài lần lặp trước thay vì lần lặp cuối cùng. Bản sao này được gọi là mạng đích.
Q-Learning là một thuật toán off-chính sách mà nghe tin về chính sách tham lam \(a = \max_{a} Q(s, a; \theta)\) trong khi sử dụng một chính sách hành vi khác nhau cho hành động trong môi trường / thu thập dữ liệu. Chính sách Hành vi này thường là một \(\epsilon\)chính sách -greedy đó chọn hành động tham lam với xác suất \(1-\epsilon\) và một hành động ngẫu nhiên với xác suất \(\epsilon\) để đảm bảo vùng phủ sóng tốt của không gian trạng thái hành động.
Trải nghiệm phát lại
Để tránh tính toán toàn bộ kỳ vọng trong tổn thất DQN, chúng ta có thể giảm thiểu nó bằng cách sử dụng phương pháp giảm độ dốc ngẫu nhiên. Nếu sự mất mát được tính bằng chỉ sự chuyển đổi cuối cùng \(\{s, a, r, s'\}\), điều này làm giảm tiêu chuẩn Q-Learning.
Công việc Atari DQN đã giới thiệu một kỹ thuật có tên là Experience Replay để làm cho các bản cập nhật mạng ổn định hơn. Tại mỗi bước thời gian thu thập dữ liệu, quá trình chuyển đổi được thêm vào một bộ đệm tròn gọi là bộ đệm phát lại. Sau đó, trong quá trình đào tạo, thay vì chỉ sử dụng quá trình chuyển đổi mới nhất để tính toán tổn thất và độ dốc của nó, chúng tôi tính toán chúng bằng cách sử dụng một loạt nhỏ các chuyển đổi được lấy mẫu từ bộ đệm phát lại. Điều này có hai lợi thế: hiệu quả dữ liệu tốt hơn bằng cách sử dụng lại mỗi chuyển đổi trong nhiều bản cập nhật và tính ổn định tốt hơn khi sử dụng các chuyển đổi không tương quan trong một đợt.
DQN trên Cartpole trong TF-Agents
TF-Agents cung cấp tất cả các thành phần cần thiết để đào tạo tác nhân DQN, chẳng hạn như bản thân tác nhân, môi trường, chính sách, mạng, bộ đệm phát lại, vòng thu thập dữ liệu và chỉ số. Các thành phần này được triển khai dưới dạng các hàm Python hoặc hoạt động biểu đồ TensorFlow và chúng tôi cũng có các trình bao bọc để chuyển đổi giữa chúng. Ngoài ra, TF-Agents hỗ trợ chế độ TensorFlow 2.0, cho phép chúng tôi sử dụng TF ở chế độ bắt buộc.
Tiếp theo, hãy xem các hướng dẫn cho việc đào tạo một tác nhân DQN đối với môi trường Cartpole sử dụng TF-Đại lý .
