Copyright 2021 Os autores do TF-Agents.
 Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Introdução
Aprendizagem por reforço (RL) é uma estrutura geral onde os agentes aprendem a realizar ações em um ambiente de forma a maximizar uma recompensa. Os dois componentes principais são o ambiente, que representa o problema a ser resolvido, e o agente, que representa o algoritmo de aprendizagem.
O agente e o ambiente interagem continuamente entre si. Em cada passo de tempo, o agente realiza uma ação sobre o meio ambiente com base em sua política \(\pi(a_t|s_t)\), onde \(s_t\) é a observação atual do meio ambiente, e recebe uma recompensa \(r_{t+1}\) ea próxima observação \(s_{t+1}\) do ambiente . O objetivo é aprimorar a política de forma a maximizar a soma das recompensas (retorno).
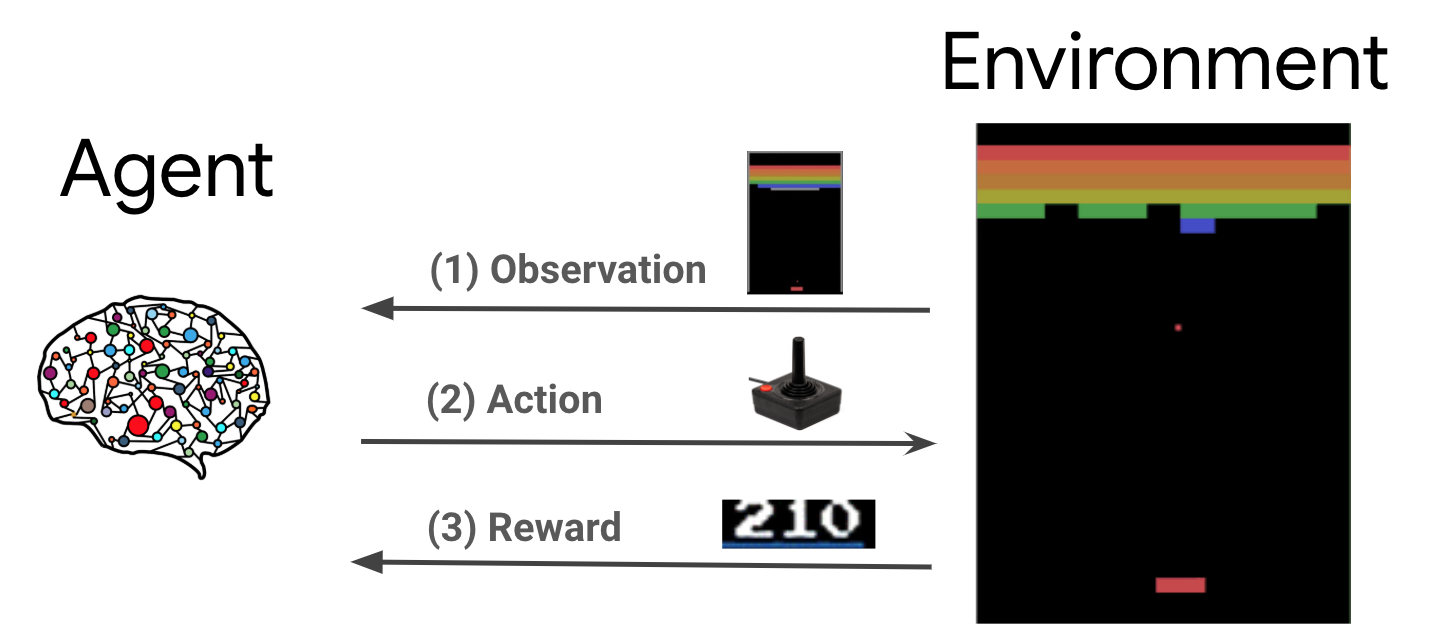
Esta é uma estrutura muito geral e pode modelar uma variedade de problemas de tomada de decisão sequencial, como jogos, robótica, etc.
O ambiente do Cartpole
O ambiente Cartpole é um dos problemas de aprendizagem reforço clássicas mais conhecidas (a "Olá, mundo!" De RL). Um mastro é preso a um carrinho, que pode se mover ao longo de uma trilha sem atrito. O mastro começa na vertical e o objetivo é evitar que ele caia controlando o carrinho.
- A observação do ambiente \(s_t\) é um vector 4D representa a posição e velocidade do carrinho, e o ângulo e a velocidade angular do poste.
- O agente pode controlar o sistema, tendo uma de 2 acções \(a_t\): empurrar o carrinho para a direita (1) ou para a esquerda (-1).
- Uma recompensa \(r_{t+1} = 1\) é fornecido para cada iteração que o pólo permanece na posição vertical. O episódio termina quando uma das seguintes opções for verdadeira:
- as pontas do pólo acima de algum limite de ângulo
- o carrinho se move para fora das bordas do mundo
- 200 passos de tempo passam.
O objetivo do agente é aprender uma política \(\pi(a_t|s_t)\) de modo a maximizar a soma de recompensas em um episódio \(\sum_{t=0}^{T} \gamma^t r_t\). Aqui \(\gamma\) é um fator de desconto em \([0, 1]\) que os descontos recompensas futuras em relação a recompensas imediatas. Esse parâmetro nos ajuda a focar a política, fazendo com que ela se preocupe mais em obter recompensas rapidamente.
O Agente DQN
O algoritmo DQN (Deep Q-Network) foi desenvolvido pela DeepMind em 2015. Ele foi capaz de resolver uma ampla gama de jogos de Atari (alguns a nível supra-humano) através da combinação de reforço de aprendizagem e redes neurais profundas em escala. O algoritmo foi desenvolvido através do reforço de um algoritmo de RL clássico chamado Q-Learning com redes neurais profundas e uma técnica chamada experiência replay.
Q-Learning
O Q-Learning é baseado na noção de uma função Q. A função Q (aka a função valor de estado-ação) de uma política \(\pi\), \(Q^{\pi}(s, a)\), mede o retorno esperado ou soma descontada de recompensas obtidas de estado \(s\) por tomar medidas \(a\) primeiro e seguindo a política \(\pi\) depois. Nós definimos o óptimo-função Q \(Q^*(s, a)\) como o retorno máxima que pode ser obtida a partir de observação \(s\), tendo acção \(a\) e seguindo a política óptima depois disso. O Q-função ideal obedece à seguinte equação optimality Bellman:
\(\begin{equation}Q^\ast(s, a) = \mathbb{E}[ r + \gamma \max_{a'} Q^\ast(s', a') ]\end{equation}\)
Isto significa que o rendimento máximo de estado \(s\) e acção \(a\) é a soma da recompensa imediata \(r\) e o retorno (descontado pelo \(\gamma\)) obtida seguindo a política óptima depois disso até o final do episódio ( ou seja, a recompensa máxima a partir do próximo estado \(s'\)). A expectativa é calculado tanto sobre a distribuição de recompensas imediatas \(r\) e possíveis estados próximos \(s'\).
A idéia básica por trás Q-Learning é usar a equação optimality Bellman como uma atualização iterativa \(Q_{i+1}(s, a) \leftarrow \mathbb{E}\left[ r + \gamma \max_{a'} Q_{i}(s', a')\right]\), e pode ser mostrado que esta converge para o ótimo \(Q\)-função, ou seja \(Q_i \rightarrow Q^*\) como \(i \rightarrow \infty\) (ver a papel DQN ).
Deep Q-Learning
Para a maioria dos problemas, é impraticável para representar o \(Q\)-função como uma tabela que contém os valores para cada combinação de \(s\) e \(a\). Em vez disso, nós treinamos uma função aproximador, tal como uma rede neural com parâmetros \(\theta\), para estimar os valores de Q, ou seja \(Q(s, a; \theta) \approx Q^*(s, a)\). Isso pode feito através da minimização do seguinte perda em cada etapa \(i\):
\(\begin{equation}L_i(\theta_i) = \mathbb{E}_{s, a, r, s'\sim \rho(.)} \left[ (y_i - Q(s, a; \theta_i))^2 \right]\end{equation}\) onde \(y_i = r + \gamma \max_{a'} Q(s', a'; \theta_{i-1})\)
Aqui, \(y_i\) é chamado o alvo TD (diferença temporal), e \(y_i - Q\) é chamado o erro TD. \(\rho\) representa a distribuição de comportamento, a distribuição ao longo transições \(\{s, a, r, s'\}\) recolhidos a partir do ambiente.
Note-se que os parâmetros da iteração anterior \(\theta_{i-1}\) são fixos e não atualizado. Na prática, usamos um instantâneo dos parâmetros de rede de algumas iterações atrás, em vez da última iteração. Essa cópia é chamado de rede de destino.
Q-Learning é um algoritmo off-política que aprende sobre a política gananciosos \(a = \max_{a} Q(s, a; \theta)\) ao usar uma política de comportamento diferente para agir no ambiente / coleta de dados. Esta política comportamento é geralmente uma \(\epsilon\)política -greedy que seleciona a ação gananciosos com probabilidade \(1-\epsilon\) e uma ação aleatória com probabilidade \(\epsilon\) para garantir uma boa cobertura do espaço de estados-action.
Experimente o Replay
Para evitar o cálculo da expectativa total na perda de DQN, podemos minimizá-la usando a descida gradiente estocástica. Se a perda é calculado usando apenas a última transição \(\{s, a, r, s'\}\), isso reduz a Q-Learning padrão.
O trabalho do Atari DQN introduziu uma técnica chamada Experience Replay para tornar as atualizações de rede mais estáveis. Em cada passo de tempo de recolha de dados, as transições são adicionados a um tampão circular chamado o tampão de repetição. Então, durante o treinamento, em vez de usar apenas a última transição para calcular a perda e seu gradiente, nós os calculamos usando um minilote de transições amostradas do buffer de reprodução. Isso tem duas vantagens: melhor eficiência de dados reutilizando cada transição em muitas atualizações e melhor estabilidade usando transições não correlacionadas em um lote.
DQN no Cartpole em TF-Agents
TF-Agents fornece todos os componentes necessários para treinar um agente DQN, como o próprio agente, o ambiente, políticas, redes, buffers de reprodução, loops de coleta de dados e métricas. Esses componentes são implementados como funções Python ou operações de gráfico TensorFlow, e também temos wrappers para conversão entre eles. Além disso, o TF-Agents é compatível com o modo TensorFlow 2.0, o que nos permite usar o TF no modo imperativo.
Em seguida, dê uma olhada no tutorial para treinar um agente DQN no ambiente Cartpole usando TF-agentes .
