Copyright 2021 Gli autori degli agenti TF.
 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza la fonte su GitHub Visualizza la fonte su GitHub |  Scarica taccuino Scarica taccuino |
introduzione
L'apprendimento per rinforzo (RL) è un quadro generale in cui gli agenti imparano a eseguire azioni in un ambiente in modo da massimizzare una ricompensa. I due componenti principali sono l'ambiente, che rappresenta il problema da risolvere, e l'agente, che rappresenta l'algoritmo di apprendimento.
L'agente e l'ambiente interagiscono continuamente tra loro. Ad ogni passo, l'agente compie un'azione sull'ambiente base alla sua politica \(\pi(a_t|s_t)\), dove \(s_t\) è la corrente osservazione dall'ambiente, e riceve un premio \(r_{t+1}\) e la successiva osservazione \(s_{t+1}\) dall'ambiente . L'obiettivo è quello di migliorare la politica in modo da massimizzare la somma delle ricompense (rendimento).
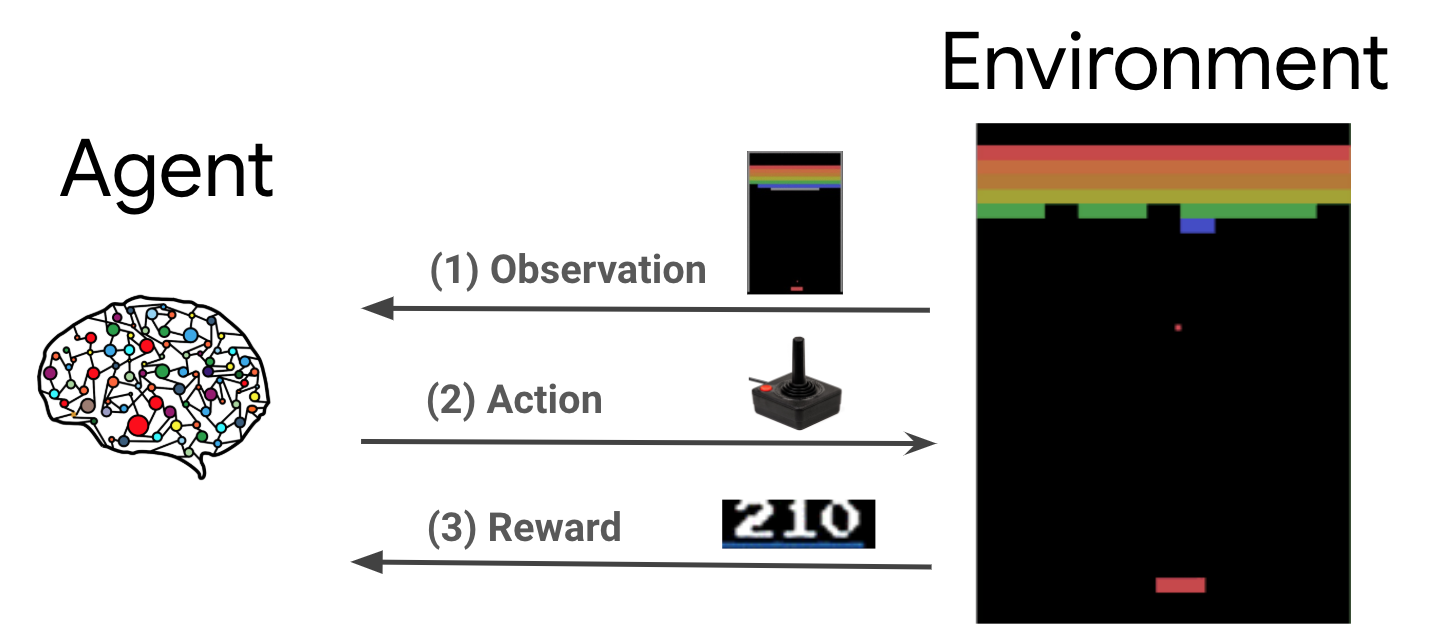
Questo è un quadro molto generale e può modellare una varietà di problemi decisionali sequenziali come giochi, robotica, ecc.
L'ambiente Cartpole
L'ambiente Cartpole è uno dei più noti problemi di apprendimento di rinforzo classici (il "Ciao, mondo!" Di RL). Un palo è attaccato a un carrello, che può muoversi lungo una pista senza attrito. Il palo parte in posizione verticale e l'obiettivo è impedire che cada controllando il carrello.
- L'osservazione dall'ambiente \(s_t\) è un vettore 4D rappresenta la posizione e la velocità del carrello, e l'angolo e la velocità angolare del polo.
- L'agente può controllare il sistema prendendo uno dei 2 azioni \(a_t\): spingere il carrello di destra (+1) oa sinistra (-1).
- Una ricompensa \(r_{t+1} = 1\) è previsto per ogni passo temporale che il polo rimane in posizione eretta. L'episodio termina quando si verifica una delle seguenti condizioni:
- il palo si inclina oltre un limite d'angolo
- il carro si muove al di fuori dei confini del mondo
- Passano 200 passi temporali.
L'obiettivo dell'agente è quello di imparare una politica \(\pi(a_t|s_t)\) in modo da massimizzare la somma di premi in un episodio \(\sum_{t=0}^{T} \gamma^t r_t\). Qui \(\gamma\) è un fattore di sconto in \([0, 1]\) che gli sconti futuri benefici relativi alle ricompense immediate. Questo parametro ci aiuta a focalizzare la politica, facendo in modo che si preoccupi maggiormente di ottenere ricompense rapidamente.
L'agente DQN
Il DQN (Deep Q-Network) algoritmo è stato sviluppato da DeepMind nel 2015. E 'stato in grado di risolvere una vasta gamma di giochi Atari (alcuni a livello sovrumano) mediante la combinazione di apprendimento per rinforzo e le reti neurali profonde su larga scala. L'algoritmo è stato sviluppato da valorizzare un algoritmo RL classico chiamato Q-Learning con le reti neurali profonde e una tecnica chiamata esperienza replay.
Q-Learning
Q-Learning si basa sulla nozione di funzione Q. Il Q-funzione (aka la funzione valore dello stato-azione) di una politica \(\pi\), \(Q^{\pi}(s, a)\), misure il rendimento atteso o somma scontata di premi ottenuti da stato \(s\) di agire \(a\) prima e dopo la politica \(\pi\) da allora in poi. Definiamo ottimale Q-funzione \(Q^*(s, a)\) come il rendimento massimo che può essere ottenibile partendo dall'osservazione \(s\), intervenendo \(a\) e seguendo l'orientamento ottimale successivamente. Il Q-funzione ottimale obbedisce alla seguente equazione ottimalità Bellman:
\(\begin{equation}Q^\ast(s, a) = \mathbb{E}[ r + \gamma \max_{a'} Q^\ast(s', a') ]\end{equation}\)
Ciò significa che il massimo ritorno da stato \(s\) e l'azione \(a\) è la somma della ricompensa immediata \(r\) e il ritorno (scontato da \(\gamma\)) ottenuta seguendo la politica ottimale da allora in poi fino alla fine della puntata ( per esempio, il premio massimo dal successivo stato \(s'\)). L'aspettativa è calcolata sia sulla distribuzione di ricompense immediate \(r\) ed eventuali successivi stati \(s'\).
L'idea alla base di Q-Learning è quello di utilizzare l'equazione ottimalita Bellman come aggiornamento iterativo \(Q_{i+1}(s, a) \leftarrow \mathbb{E}\left[ r + \gamma \max_{a'} Q_{i}(s', a')\right]\), e si può dimostrare che questi converge alla ottimale \(Q\)-funzione, cioè \(Q_i \rightarrow Q^*\) come \(i \rightarrow \infty\) (vedi la carta DQN ).
Q-learning profondo
Per la maggior parte dei problemi, non è pratico per rappresentare il \(Q\)-funzione come una tabella contenente i valori per ogni combinazione di \(s\) e \(a\). Invece, formiamo una funzione approssimatore, come una rete neurale con parametri \(\theta\), per stimare i valori di Q, cioè \(Q(s, a; \theta) \approx Q^*(s, a)\). Questo può fatto minimizzando la seguente perdita ad ogni passo \(i\):
\(\begin{equation}L_i(\theta_i) = \mathbb{E}_{s, a, r, s'\sim \rho(.)} \left[ (y_i - Q(s, a; \theta_i))^2 \right]\end{equation}\) dove \(y_i = r + \gamma \max_{a'} Q(s', a'; \theta_{i-1})\)
Qui, \(y_i\) è chiamato il bersaglio TD (differenza temporale), e \(y_i - Q\) si chiama l'errore TD. \(\rho\) rappresenta la distribuzione comportamento, la distribuzione sulle transizioni \(\{s, a, r, s'\}\) raccolti dall'ambiente.
Si noti che i parametri della precedente iterazione \(\theta_{i-1}\) sono fissi e non aggiornati. In pratica usiamo un'istantanea dei parametri di rete di poche iterazioni fa invece dell'ultima iterazione. Questa copia è chiamata la rete di destinazione.
Q-Learning è un algoritmo off-politica che impara a conoscere la politica avida \(a = \max_{a} Q(s, a; \theta)\) mentre si utilizza un criterio diverso comportamento per agire in ambiente / la raccolta dei dati. Questa politica comportamento è di solito un \(\epsilon\)politica -greedy che seleziona l'azione avido con probabilità \(1-\epsilon\) e un'azione casuale con probabilità \(\epsilon\) per garantire una buona copertura dello spazio degli stati-azione.
Replay dell'esperienza
Per evitare di calcolare l'aspettativa completa nella perdita DQN, possiamo minimizzarla usando la discesa del gradiente stocastico. Se la perdita è calcolata utilizzando solo l'ultimo passaggio \(\{s, a, r, s'\}\), questo riduce lo standard Q-Learning.
Il lavoro di Atari DQN ha introdotto una tecnica chiamata Experience Replay per rendere più stabili gli aggiornamenti di rete. Ad ogni passo della raccolta dei dati, le transizioni vengono aggiunti a un buffer circolare chiamato buffer di riproduzione. Quindi, durante l'addestramento, invece di utilizzare solo l'ultima transizione per calcolare la perdita e il suo gradiente, li calcoliamo utilizzando un mini batch di transizioni campionate dal buffer di riproduzione. Ciò ha due vantaggi: una migliore efficienza dei dati riutilizzando ogni transizione in molti aggiornamenti e una migliore stabilità utilizzando transizioni non correlate in un batch.
DQN su Cartpole in TF-Agenti
TF-Agents fornisce tutti i componenti necessari per addestrare un agente DQN, come l'agente stesso, l'ambiente, le politiche, le reti, i buffer di riproduzione, i cicli di raccolta dati e le metriche. Questi componenti sono implementati come funzioni Python o operazioni grafiche TensorFlow e abbiamo anche wrapper per la conversione tra di loro. Inoltre, TF-Agents supporta la modalità TensorFlow 2.0, che ci consente di utilizzare TF in modalità imperativa.
Avanti, date un'occhiata al tutorial per la formazione di un agente DQN sull'ambiente Cartpole utilizzando TF-Agenti .
