זכויות יוצרים 2021 מחברי TF-Agents.
 הצג באתר TensorFlow.org הצג באתר TensorFlow.org |  הפעל בגוגל קולאב הפעל בגוגל קולאב |  צפה במקור ב-GitHub צפה במקור ב-GitHub |  הורד מחברת הורד מחברת |
מבוא
למידת חיזוק (RL) היא מסגרת כללית שבה סוכנים לומדים לבצע פעולות בסביבה כדי למקסם את התגמול. שני המרכיבים העיקריים הם הסביבה, המייצגת את הבעיה שיש לפתור, והסוכן, המייצג את אלגוריתם הלמידה.
הסוכן והסביבה מקיימים אינטראקציה מתמשכת זה עם זה. בכל שלב בזמן, הסוכן נוקט פעולה הסביבה המבוססת על מדיניותו \(\pi(a_t|s_t)\), שבו \(s_t\) היא התצפית הנוכחית מהסביבה, ומקבל גמול \(r_{t+1}\) ואת התצפית הבאה \(s_{t+1}\) מהסביבה . המטרה היא לשפר את הפוליסה כדי למקסם את סכום התגמולים (החזר).
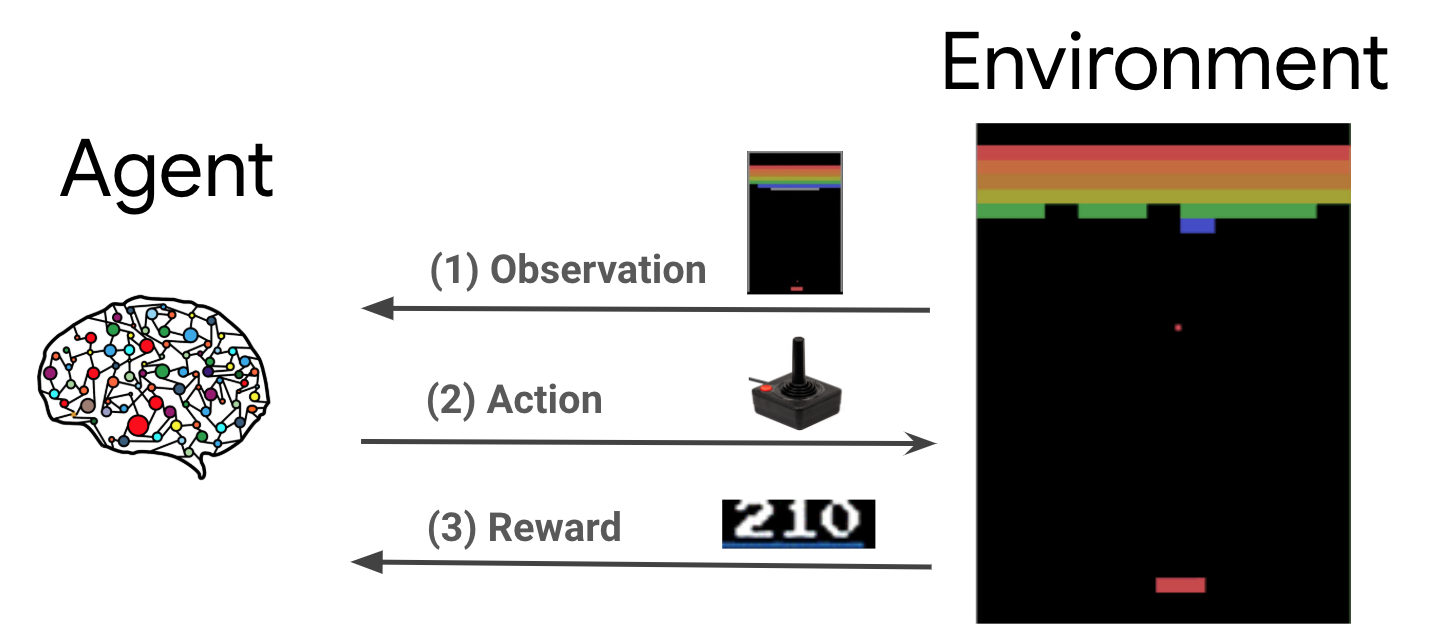
זוהי מסגרת כללית מאוד ויכולה לדגמן מגוון בעיות של קבלת החלטות ברצף כמו משחקים, רובוטיקה וכו'.
סביבת הקרטון
סביבת Cartpole היא אחת הבעיות למידה חיזוק קלאסי הידועים ביותר (להלן: "שלום, עולם!" של RL). מוט מחובר לעגלה, שיכול לנוע לאורך מסילה ללא חיכוך. המוט מתחיל זקוף והמטרה היא למנוע ממנו ליפול על ידי שליטה בעגלה.
- תצפית מהסביבה \(s_t\) הוא וקטור 4D המייצג את המיקום והמהירות של העגלה, ואת הזווית ואת המהירות הזוויתית של המוט.
- הסוכן יכול לשלוט על המערכת על ידי לקיחת אחד 2 פעולות \(a_t\): לדחוף את הזכות עגלת (1) או שמאלה (-1).
- גמול \(r_{t+1} = 1\) מסופק לכל timestep כי הקוטב נשאר זקוף. הפרק מסתיים כאשר אחד מהדברים הבאים נכון:
- המוט נוטה מעל מגבלת זווית כלשהי
- העגלה נעה מחוץ לקצוות העולם
- עוברים 200 צעדי זמן.
מטרת הסוכן הוא ללמוד מדיניות \(\pi(a_t|s_t)\) מנת למקסם את סכום התגמולים ב אפיזודה \(\sum_{t=0}^{T} \gamma^t r_t\). הנה \(\gamma\) הוא מקדם ההיוון ב \([0, 1]\) כי בעתיד הנחות מתגמלת ביחס תגמולים מיידיים. פרמטר זה עוזר לנו למקד את המדיניות, מה שגורם לה לדאוג יותר להשגת תגמולים במהירות.
סוכן DQN
DQN (Deep Q-Network) האלגוריתם שפותח על ידי DeepMind בשנת 2015. זה היה מסוגל לפתור מגוון רחב של משחקי עטרי (כמה לרמה על-אנושית) על ידי שילוב למידת חיזוק ורשתות עצביות עמוקות בקנה מידה. האלגוריתם שפותח על ידי שיפור אלגוריתם RL קלסי שנקרא Q-Learning עם רשתות עצביות עמוקות חוזר חוויה שנקראת טכניקה.
Q-Learning
Q-Learning מבוסס על הרעיון של פונקציית Q. Q-פונקציה (aka הפונקציה ערך המדינה- פעולה) של מדיניות \(\pi\), \(Q^{\pi}(s, a)\)סכום, מודד את התשואה הצפויה או בהנחה של תגמולים המתקבלים המדינה \(s\) ידי נקיטת פעולה \(a\) הראשון ובעקבות מדיניות \(\pi\) ואילך. אנו מגדירים את Q-תפקוד אופטימלי \(Q^*(s, a)\) כמו התשואה המקסימלית שניתן להשיג החל תצפית \(s\), נקיטת פעולה \(a\) ובעקבות מדיניות אופטימלית לאחר מכן. The-פונקצית Q אופטימאלי מציית המשוואה אופטימאלי בלמן הבא:
\(\begin{equation}Q^\ast(s, a) = \mathbb{E}[ r + \gamma \max_{a'} Q^\ast(s', a') ]\end{equation}\)
אמצעי זה כי את התשואה המקסימלית ממצב \(s\) ופעולה \(a\) הוא סכום הפרס המיידי \(r\) והחזרת (עם הפחתת \(\gamma\)) המתקבל על ידי ביצוע מדיניות אופטימלית מכן עד סוף הפרק ( כלומר, את הפרס המקסימאלי מהמדינה הבאה \(s'\)). הציפייה חושב היא על חלוק תגמולים המיידיים \(r\) והמדינות הבאות אפשריות \(s'\).
הרעיון הבסיסי מאחורי Q-למידה היא להשתמש במשוואה האופטימליות בלמן כעדכון איטרטיבי \(Q_{i+1}(s, a) \leftarrow \mathbb{E}\left[ r + \gamma \max_{a'} Q_{i}(s', a')\right]\), וזה יכול להיות הראו כי מתכנס זו אל אופטימלי \(Q\)-function, כלומר \(Q_i \rightarrow Q^*\) כמו \(i \rightarrow \infty\) (ראה DQN נייר ).
Deep Q-Learning
עבור רוב הבעיות, זה מעשי לייצג את \(Q\)-function כטבלה המכיל ערכים עבור כל שילוב של \(s\) ו \(a\). במקום זאת, אנו מאמנים פונקציה approximator, כגון רשת עצבית עם פרמטרים \(\theta\), כדי לאמוד את Q-ערכי, כלומר \(Q(s, a; \theta) \approx Q^*(s, a)\). זה יכול להיעשות על ידי מזעור ההפסד הבא בכול שלב \(i\):
\(\begin{equation}L_i(\theta_i) = \mathbb{E}_{s, a, r, s'\sim \rho(.)} \left[ (y_i - Q(s, a; \theta_i))^2 \right]\end{equation}\) שבו \(y_i = r + \gamma \max_{a'} Q(s', a'; \theta_{i-1})\)
הנה, \(y_i\) נקרא TD (הבדל זמני) היעד, ועל \(y_i - Q\) נקראת שגיאת TD. \(\rho\) מייצג את הפצת ההתנהגות, חלוק מעל מעברי \(\{s, a, r, s'\}\) שנאספו מהסביבה.
שים לב לפרמטרים מן איטרציה הקודמת \(\theta_{i-1}\) שתוקנו ולא מעודכנים. בפועל אנו משתמשים בתמונת מצב של פרמטרי הרשת מלפני מספר איטרציות במקום האיטרציה האחרונה. עותק זה נקרא רשת היעד.
Q-למידה הוא אלגוריתם מחוץ מדיניות לומד על מדיניות חמדן \(a = \max_{a} Q(s, a; \theta)\) תוך שימוש במדיניות התנהגות שונה עבור מתנהג בסביבה / איסוף נתונים. מדיניות התנהגות זו היא בדרך כלל \(\epsilon\)מדיניות -greedy הבוחרת את הפעולה חמדן עם הסתברות \(1-\epsilon\) לבין פעולה אקראית עם הסתברות \(\epsilon\) כדי להבטיח כיסוי טוב של המרחב-פעולה המדינה.
חווה משחק חוזר
כדי להימנע מחישוב הציפיות המלאות באובדן DQN, נוכל למזער אותה באמצעות ירידה בשיפוע סטוכסטי. אם ההפסד מחושבת באמצעות רק את המעבר האחרון \(\{s, a, r, s'\}\), זה מפחית את-למידה Q סטנדרטי.
עבודת Atari DQN הציגה טכניקה בשם Experience Replay כדי להפוך את עדכוני הרשת ליציבים יותר. בכל שלב בעת איסוף הנתונים, המעברים מתווספים למאגר מעגלית המכונה חוצץ החוזר. ואז במהלך האימון, במקום להשתמש רק במעבר האחרון כדי לחשב את ההפסד והשיפוע שלו, אנו מחשבים אותם באמצעות מיני-אצט של מעברים שנדגמו מהמאגר החוזר. יש לכך שני יתרונות: יעילות נתונים טובה יותר על ידי שימוש חוזר בכל מעבר בעדכונים רבים, ויציבות טובה יותר באמצעות מעברים לא מתואמים באצווה.
DQN על Cartpole ב-TF-Agents
TF-Agents מספק את כל הרכיבים הדרושים להכשרת סוכן DQN, כגון הסוכן עצמו, הסביבה, מדיניות, רשתות, מאגרי הפעלה חוזרת, לולאות איסוף נתונים ומדדים. רכיבים אלו מיושמים כפונקציות Python או TensorFlow graph ops, ויש לנו גם עטיפות להמרה ביניהם. בנוסף, TF-Agents תומך במצב TensorFlow 2.0, המאפשר לנו להשתמש ב-TF במצב חיוני.
הבא, תסתכל על ההדרכה להכשרת סוכן DQN על סביבת Cartpole באמצעות-סוכני TF .
