Copyright 2021 Les auteurs TF-Agents.
 Voir sur TensorFlow.org |  Exécuter dans Google Colab |  Voir la source sur GitHub |  Télécharger le cahier |
introduction
L'apprentissage par renforcement (RL) est un cadre général dans lequel les agents apprennent à effectuer des actions dans un environnement afin de maximiser une récompense. Les deux composants principaux sont l'environnement, qui représente le problème à résoudre, et l'agent, qui représente l'algorithme d'apprentissage.
L'agent et l'environnement interagissent en permanence les uns avec les autres. A chaque pas de temps, l'agent effectue une action sur l'environnement sur la base de sa politique \(\pi(a_t|s_t)\), où \(s_t\) est l'observation courante à partir de l'environnement, et reçoit une récompense \(r_{t+1}\) et l'observation suivante \(s_{t+1}\) de l'environnement . L'objectif est d'améliorer la politique de manière à maximiser la somme des récompenses (retour).
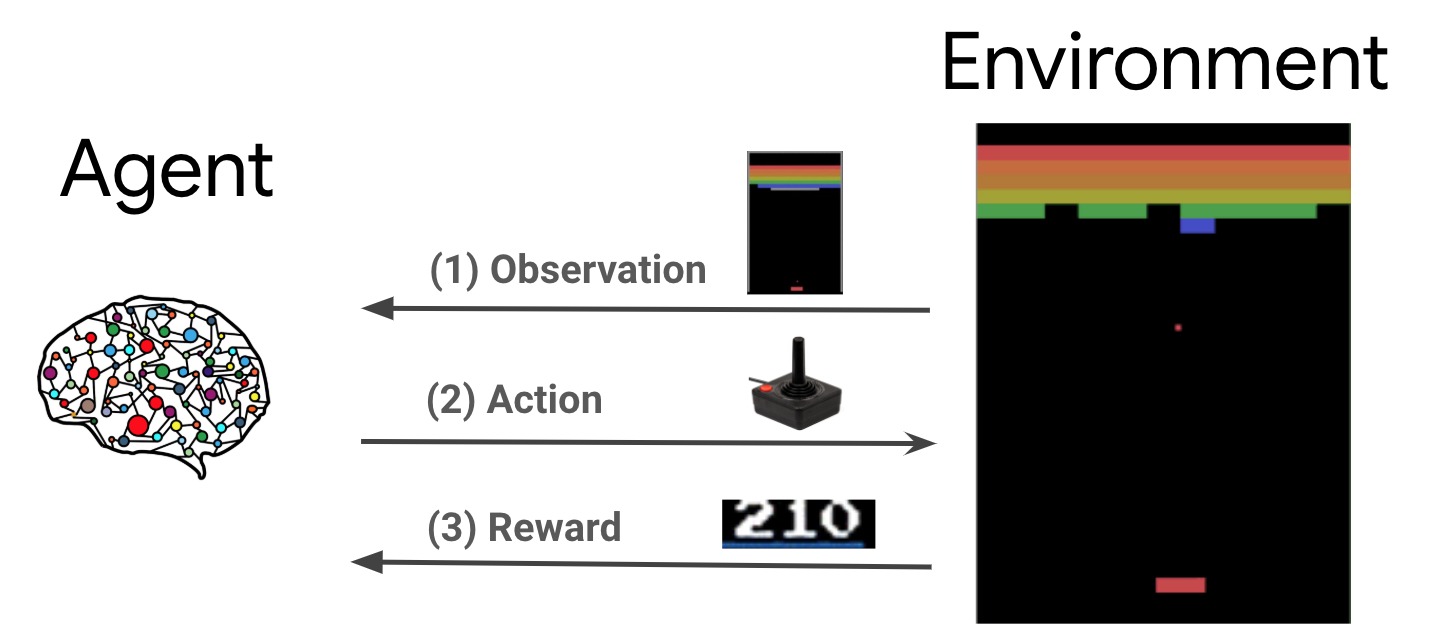
Il s'agit d'un cadre très général et peut modéliser une variété de problèmes de prise de décision séquentielle tels que les jeux, la robotique, etc.
L'environnement Cartpole
L'environnement Cartpole est l' un des plus connus des problèmes d'apprentissage de renforcement classique (le « Bonjour, monde! » De RL). Un poteau est attaché à un chariot, qui peut se déplacer le long d'une piste sans friction. La perche démarre debout et le but est de l'empêcher de tomber en contrôlant le chariot.
- L'observation de l'environnement \(s_t\) est un vecteur 4D représentant la position et la vitesse du chariot, et l'angle et la vitesse angulaire de la perche.
- L'agent peut contrôler le système en prenant l' une des 2 actions \(a_t\): pousser le droit du chariot (1) ou à gauche (-1).
- Une récompense \(r_{t+1} = 1\) est fourni pour chaque timestep que le pôle reste debout. L'épisode se termine lorsque l'une des conditions suivantes est vraie :
- le pôle bascule sur une certaine limite d'angle
- le chariot se déplace en dehors des bords du monde
- 200 pas de temps passent.
Le but de l'agent est d'apprendre une politique \(\pi(a_t|s_t)\) de manière à maximiser la somme des récompenses dans un épisode \(\sum_{t=0}^{T} \gamma^t r_t\). Ici \(\gamma\) est un facteur d'actualisation dans \([0, 1]\) que l' avenir de rabais récompense par rapport à des récompenses immédiates. Ce paramètre nous aide à cibler la politique, ce qui la rend plus soucieuse d'obtenir des récompenses rapidement.
L'agent DQN
Le DQN algorithme (Deep Q-réseau) a été développé par DeepMind en 2015. Il a été en mesure de résoudre un large éventail de jeux Atari ( dont certains à un niveau surhumain) en combinant l' apprentissage de renforcement et les réseaux de neurones profonds à l' échelle. L'algorithme a été développé par l' amélioration d' un algorithme de RL classique appelé Q-Learning avec les réseaux de neurones profonds et une rediffusion de l' expérience technique appelée.
Q-Apprentissage
Q-Learning est basé sur la notion de fonction Q. Le Q-fonction (alias la fonction de la valeur de l' action publique) d'une politique \(\pi\), \(Q^{\pi}(s, a)\), mesure le rendement prévu ou somme actualisée des récompenses obtenues à partir de l' état \(s\) en prenant des mesures \(a\) premier et suivant la politique \(\pi\) par la suite. Nous définissons la fonction Q optimale \(Q^*(s, a)\) que le rendement maximal qui peut être obtenu à partir de l' observation \(s\), prendre des mesures \(a\) et suivant la politique optimale par la suite. Le Q-fonction optimale obéit à l'équation d'optimalité de Bellman suivante:
\(\begin{equation}Q^\ast(s, a) = \mathbb{E}[ r + \gamma \max_{a'} Q^\ast(s', a') ]\end{equation}\)
Cela signifie que le rendement maximal de l' état \(s\) et de l' action \(a\) est la somme de la récompense immédiate \(r\) et le retour (actualisé par \(\gamma\)) obtenu en suivant la politique optimale par la suite jusqu'à la fin de l'épisode ( à savoir, la récompense maximale de l'état suivant \(s'\)). L'attente est calculée à la fois sur la distribution des récompenses immédiates \(r\) et états suivants possibles \(s'\).
L'idée de base Q-Learning est d'utiliser l'équation d'optimalité Bellman comme une mise à jour itérative \(Q_{i+1}(s, a) \leftarrow \mathbb{E}\left[ r + \gamma \max_{a'} Q_{i}(s', a')\right]\), et il peut être démontré que ce converge vers la valeur optimale \(Q\)-fonction, à savoir \(Q_i \rightarrow Q^*\) comme \(i \rightarrow \infty\) (voir la papier DQN ).
Apprentissage Q approfondi
Pour la plupart des problèmes, il est impossible de représenter le \(Q\)-fonction comme une table contenant des valeurs pour chaque combinaison de \(s\) et \(a\). Au lieu de cela, on forme une approximation de fonction, tel qu'un réseau de neurones avec des paramètres \(\theta\), pour estimer les valeurs de Q, soit \(Q(s, a; \theta) \approx Q^*(s, a)\). Cela peut faire en réduisant au minimum la perte suivante à chaque étape \(i\):
\(\begin{equation}L_i(\theta_i) = \mathbb{E}_{s, a, r, s'\sim \rho(.)} \left[ (y_i - Q(s, a; \theta_i))^2 \right]\end{equation}\) où \(y_i = r + \gamma \max_{a'} Q(s', a'; \theta_{i-1})\)
Ici, \(y_i\) est appelé la cible TD (différence temporelle), et \(y_i - Q\) est appelé l'erreur TD. \(\rho\) représente la distribution du comportement, la répartition sur les transitions \(\{s, a, r, s'\}\) recueillies de l'environnement.
Notez que les paramètres de la précédente itération \(\theta_{i-1}\) sont fixes et non mis à jour. En pratique, nous utilisons un instantané des paramètres réseau d'il y a quelques itérations au lieu de la dernière itération. Cette copie est appelée le réseau cible.
Q-apprentissage est un algorithme hors politique qui apprend la politique avide \(a = \max_{a} Q(s, a; \theta)\) tout en utilisant une politique de comportement différent pour agir dans l'environnement / collecte de données. Cette politique de comportement est généralement un \(\epsilon\)politique -greedy qui choisit l'action gourmande avec une probabilité \(1-\epsilon\) et une action aléatoire avec une probabilité \(\epsilon\) pour assurer une bonne couverture de l'espace state-action.
Rejouer l'expérience
Pour éviter de calculer l'espérance complète de la perte DQN, nous pouvons la minimiser en utilisant la descente de gradient stochastique. Si la perte est calculée en utilisant seulement la dernière transition \(\{s, a, r, s'\}\), ce qui réduit à Q-Learning standard.
Le travail d'Atari DQN a introduit une technique appelée Experience Replay pour rendre les mises à jour du réseau plus stables. A chaque pas de temps de collecte de données, les transitions sont ajoutés à un tampon circulaire appelé le tampon de lecture. Ensuite, pendant l'apprentissage, au lieu d'utiliser uniquement la dernière transition pour calculer la perte et son gradient, nous les calculons à l'aide d'un mini-lot de transitions échantillonnées à partir du tampon de relecture. Cela présente deux avantages : une meilleure efficacité des données en réutilisant chaque transition dans de nombreuses mises à jour et une meilleure stabilité en utilisant des transitions non corrélées dans un lot.
DQN sur Cartpole dans TF-Agents
TF-Agents fournit tous les composants nécessaires pour former un agent DQN, tels que l'agent lui-même, l'environnement, les politiques, les réseaux, les tampons de relecture, les boucles de collecte de données et les métriques. Ces composants sont implémentés en tant que fonctions Python ou opérations graphiques TensorFlow, et nous avons également des wrappers pour la conversion entre eux. De plus, TF-Agents prend en charge le mode TensorFlow 2.0, ce qui nous permet d'utiliser TF en mode impératif.
Ensuite, jetez un oeil au tutoriel pour la formation d' un agent DQN sur l'environnement Cartpole utilisant TF-agents .