Copyright 2021 Los autores de TF-Agents.
 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar cuaderno Descargar cuaderno |
Introducción
El aprendizaje por refuerzo (RL) es un marco general donde los agentes aprenden a realizar acciones en un entorno para maximizar una recompensa. Los dos componentes principales son el entorno, que representa el problema a resolver, y el agente, que representa el algoritmo de aprendizaje.
El agente y el entorno interactúan continuamente entre sí. En cada paso de tiempo, el agente toma una acción sobre el medio ambiente sobre la base de su política \(\pi(a_t|s_t)\), donde \(s_t\) es la observación actual desde el medio ambiente, y recibe una recompensa \(r_{t+1}\) y la siguiente observación \(s_{t+1}\) desde el entorno . El objetivo es mejorar la política para maximizar la suma de recompensas (retorno).
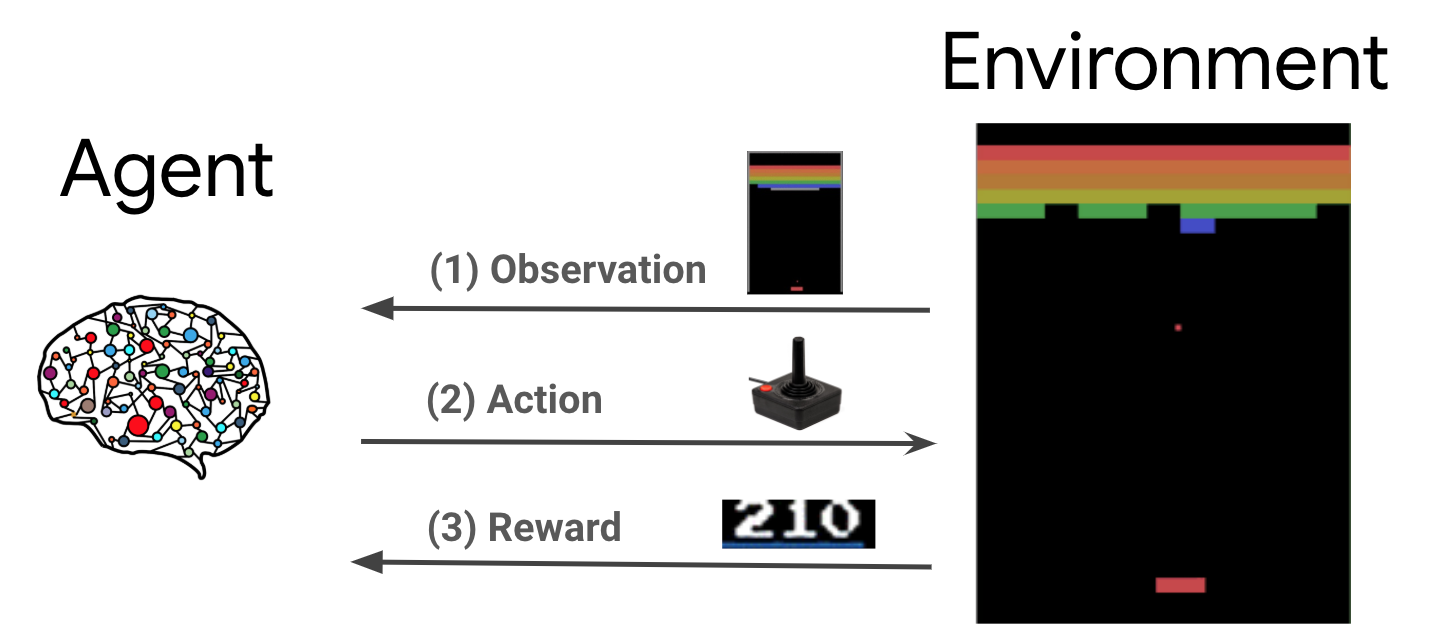
Este es un marco muy general y puede modelar una variedad de problemas de toma de decisiones secuenciales, como juegos, robótica, etc.
El entorno de Cartpole
El entorno Cartpole es uno de los problemas de aprendizaje de refuerzo clásicos más conocidos (el "Hola, mundo!" De RL). Un poste está sujeto a un carro, que puede moverse a lo largo de una pista sin fricción. El poste comienza en posición vertical y el objetivo es evitar que se caiga controlando el carro.
- La observación del entorno \(s_t\) es un vector 4D representa la posición y la velocidad del carro, y el ángulo y la velocidad angular del polo.
- El agente puede controlar el sistema mediante la adopción de uno de los 2 acciones \(a_t\): empujar la derecha de la compra (1) o izquierda (-1).
- Una recompensa \(r_{t+1} = 1\) se proporciona para cada paso de tiempo que el polo permanece en posición vertical. El episodio termina cuando se cumple una de las siguientes situaciones:
- el poste se inclina por encima de algún límite de ángulo
- el carro se mueve fuera de los bordes del mundo
- Pasan 200 pasos de tiempo.
El objetivo del agente es aprender una política \(\pi(a_t|s_t)\) a fin de maximizar la suma de recompensas en un episodio \(\sum_{t=0}^{T} \gamma^t r_t\). Aquí \(\gamma\) es un factor de descuento en \([0, 1]\) que los descuentos recompensas futuras en relación con recompensas inmediatas. Este parámetro nos ayuda a enfocar la política, haciendo que se preocupe más por obtener recompensas rápidamente.
El agente DQN
El DQN (Deep Q-Red) algoritmo fue desarrollado por DeepMind en 2015. Fue capaz de resolver una amplia gama de juegos de Atari (algunos a nivel sobrehumano) mediante la combinación de aprendizaje por refuerzo y redes neuronales profundas a gran escala. El algoritmo fue desarrollado por la mejora de un algoritmo de RL clásico llamado Q-aprendizaje con redes neuronales profundos y una técnica llamada experiencia de reproducción.
Q-Learning
Q-Learning se basa en la noción de función Q. El Q-función (también conocido como la función de valor de estado-acción) de una política \(\pi\), \(Q^{\pi}(s, a)\), las medidas del rendimiento esperado o suma descontada de las recompensas obtenidas de un estado \(s\) por la adopción de medidas \(a\) primera y siguiendo la política \(\pi\) partir de entonces. Definimos el óptimo Q-función \(Q^*(s, a)\) como el retorno máximo que se puede obtener a partir de la observación \(s\), la adopción de medidas \(a\) y siguiendo la política óptima a partir de entonces. El Q-función óptima obedece a la siguiente ecuación optimalidad de Bellman:
\(\begin{equation}Q^\ast(s, a) = \mathbb{E}[ r + \gamma \max_{a'} Q^\ast(s', a') ]\end{equation}\)
Esto significa que el máximo retorno de estado \(s\) y la acción \(a\) es la suma de la recompensa inmediata \(r\) y el retorno (descontado por \(\gamma\)) obtenido siguiendo la política óptima a partir de entonces hasta el final del episodio ( es decir, la recompensa máxima desde el estado siguiente \(s'\)). La expectativa se calcula tanto sobre la distribución de recompensas inmediatas \(r\) y posibles estados próximos \(s'\).
La idea básica detrás de Q-aprendizaje es el uso de la ecuación de optimalidad de Bellman como una actualización iterativa \(Q_{i+1}(s, a) \leftarrow \mathbb{E}\left[ r + \gamma \max_{a'} Q_{i}(s', a')\right]\), y se puede demostrar que esta converge al óptimo \(Q\)-función, es decir \(Q_i \rightarrow Q^*\) como \(i \rightarrow \infty\) (ver la papel DQN ).
Q-Learning profundo
Para la mayoría de los problemas, no es práctico para representar la \(Q\)-Función como una tabla que contiene valores para cada combinación de \(s\) y \(a\). En su lugar, formamos un aproximador función, tal como una red neuronal con parámetros \(\theta\), para estimar los valores de Q, es decir, \(Q(s, a; \theta) \approx Q^*(s, a)\). Esto puede hacerse mediante la minimización de la siguiente pérdida en cada paso \(i\):
\(\begin{equation}L_i(\theta_i) = \mathbb{E}_{s, a, r, s'\sim \rho(.)} \left[ (y_i - Q(s, a; \theta_i))^2 \right]\end{equation}\) donde \(y_i = r + \gamma \max_{a'} Q(s', a'; \theta_{i-1})\)
Aquí, \(y_i\) se llama la TD (diferencia temporal) de destino, y \(y_i - Q\) se llama el error TD. \(\rho\) representa la distribución comportamiento, la distribución a través de las transiciones \(\{s, a, r, s'\}\) recogidos del medio ambiente.
Tenga en cuenta que los parámetros de la iteración anterior \(\theta_{i-1}\) son fijos y no se actualizan. En la práctica, usamos una instantánea de los parámetros de red de algunas iteraciones atrás en lugar de la última iteración. Esta copia se llama la red de destino.
Q-aprendizaje es un algoritmo fuera de la política que aprende sobre la política codiciosa \(a = \max_{a} Q(s, a; \theta)\) durante el uso de una política de comportamiento diferente para actuar en el entorno / recepción de datos. Esta política comportamiento es por lo general un \(\epsilon\)política -greedy que selecciona la acción codiciosos con probabilidad \(1-\epsilon\) y una acción aleatoria con probabilidad \(\epsilon\) para asegurar una buena cobertura del espacio de estado-acción.
Experiencia de repetición
Para evitar calcular la expectativa total en la pérdida de DQN, podemos minimizarla usando el descenso de gradiente estocástico. Si la pérdida se calcula utilizando sólo la última transición \(\{s, a, r, s'\}\), esto se reduce a Q-Learning estándar.
El trabajo de Atari DQN introdujo una técnica llamada Experience Replay para hacer que las actualizaciones de la red sean más estables. En cada paso de tiempo de recopilación de datos, las transiciones se añaden a un buffer circular llamada la memoria intermedia de reproducción. Luego, durante el entrenamiento, en lugar de usar solo la última transición para calcular la pérdida y su gradiente, los calculamos usando un mini-lote de transiciones muestreadas del búfer de reproducción. Esto tiene dos ventajas: una mejor eficiencia de los datos al reutilizar cada transición en muchas actualizaciones y una mejor estabilidad al usar transiciones no correlacionadas en un lote.
DQN en Cartpole en TF-Agents
TF-Agents proporciona todos los componentes necesarios para capacitar a un agente DQN, como el propio agente, el entorno, las políticas, las redes, los búferes de reproducción, los bucles de recopilación de datos y las métricas. Estos componentes se implementan como funciones de Python o operaciones gráficas de TensorFlow, y también tenemos contenedores para convertir entre ellos. Además, TF-Agents admite el modo TensorFlow 2.0, que nos permite usar TF en modo imperativo.
A continuación, echar un vistazo a la clase particular para la formación de un agente DQN sobre el medio ambiente Cartpole usando TF-Agentes .
