 Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Visão geral
Este tutorial demonstra o uso da Taxa de aprendizagem cíclica do pacote de complementos.
Taxas de aprendizagem cíclica
Foi demonstrado que é benéfico ajustar a taxa de aprendizagem à medida que o treinamento progride para uma rede neural. Ele tem vários benefícios que vão desde a recuperação do ponto de sela até a prevenção de instabilidades numéricas que podem surgir durante a retropropagação. Mas como saber quanto ajustar em relação a um determinado carimbo de data / hora de treinamento? Em 2015, Leslie Smith percebeu que você gostaria de aumentar a taxa de aprendizado para atravessar mais rápido o cenário de perdas, mas também reduziria a taxa de aprendizado ao se aproximar da convergência. Para concretizar esta ideia, ele propôs Cyclical Aprendizagem Preços (CLR) onde você iria ajustar a taxa de aprendizagem em relação aos ciclos de uma função. Para uma demonstração visual, você pode conferir neste blog . CLR agora está disponível como uma API TensorFlow. Para mais detalhes, veja o artigo original aqui .
Configurar
pip install -q -U tensorflow_addons
from tensorflow.keras import layers
import tensorflow_addons as tfa
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
tf.random.set_seed(42)
np.random.seed(42)
Carregar e preparar o conjunto de dados
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
x_train = np.expand_dims(x_train, -1)
x_test = np.expand_dims(x_test, -1)
Definir hiperparâmetros
BATCH_SIZE = 64
EPOCHS = 10
INIT_LR = 1e-4
MAX_LR = 1e-2
Definir a construção de modelos e utilitários de treinamento de modelos
def get_training_model():
model = tf.keras.Sequential(
[
layers.InputLayer((28, 28, 1)),
layers.experimental.preprocessing.Rescaling(scale=1./255),
layers.Conv2D(16, (5, 5), activation="relu"),
layers.MaxPooling2D(pool_size=(2, 2)),
layers.Conv2D(32, (5, 5), activation="relu"),
layers.MaxPooling2D(pool_size=(2, 2)),
layers.SpatialDropout2D(0.2),
layers.GlobalAvgPool2D(),
layers.Dense(128, activation="relu"),
layers.Dense(10, activation="softmax"),
]
)
return model
def train_model(model, optimizer):
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer,
metrics=["accuracy"])
history = model.fit(x_train,
y_train,
batch_size=BATCH_SIZE,
validation_data=(x_test, y_test),
epochs=EPOCHS)
return history
No interesse da reprodutibilidade, os pesos do modelo inicial são serializados, os quais você usará para conduzir nossos experimentos.
initial_model = get_training_model()
initial_model.save("initial_model")
WARNING:tensorflow:Compiled the loaded model, but the compiled metrics have yet to be built. `model.compile_metrics` will be empty until you train or evaluate the model. 2021-11-12 19:14:52.355642: W tensorflow/python/util/util.cc:368] Sets are not currently considered sequences, but this may change in the future, so consider avoiding using them. INFO:tensorflow:Assets written to: initial_model/assets
Treine um modelo sem CLR
standard_model = tf.keras.models.load_model("initial_model")
no_clr_history = train_model(standard_model, optimizer="sgd")
WARNING:tensorflow:No training configuration found in save file, so the model was *not* compiled. Compile it manually. Epoch 1/10 938/938 [==============================] - 5s 4ms/step - loss: 2.2089 - accuracy: 0.2180 - val_loss: 1.7581 - val_accuracy: 0.4137 Epoch 2/10 938/938 [==============================] - 3s 3ms/step - loss: 1.2951 - accuracy: 0.5136 - val_loss: 0.9583 - val_accuracy: 0.6491 Epoch 3/10 938/938 [==============================] - 3s 3ms/step - loss: 1.0096 - accuracy: 0.6189 - val_loss: 0.9155 - val_accuracy: 0.6588 Epoch 4/10 938/938 [==============================] - 3s 3ms/step - loss: 0.9269 - accuracy: 0.6572 - val_loss: 0.8495 - val_accuracy: 0.7011 Epoch 5/10 938/938 [==============================] - 3s 3ms/step - loss: 0.8855 - accuracy: 0.6722 - val_loss: 0.8361 - val_accuracy: 0.6685 Epoch 6/10 938/938 [==============================] - 3s 3ms/step - loss: 0.8482 - accuracy: 0.6852 - val_loss: 0.7975 - val_accuracy: 0.6830 Epoch 7/10 938/938 [==============================] - 3s 3ms/step - loss: 0.8219 - accuracy: 0.6941 - val_loss: 0.7630 - val_accuracy: 0.6990 Epoch 8/10 938/938 [==============================] - 3s 3ms/step - loss: 0.7995 - accuracy: 0.7011 - val_loss: 0.7280 - val_accuracy: 0.7263 Epoch 9/10 938/938 [==============================] - 3s 3ms/step - loss: 0.7830 - accuracy: 0.7059 - val_loss: 0.7156 - val_accuracy: 0.7445 Epoch 10/10 938/938 [==============================] - 3s 3ms/step - loss: 0.7636 - accuracy: 0.7136 - val_loss: 0.7026 - val_accuracy: 0.7462
Definir cronograma CLR
O tfa.optimizers.CyclicalLearningRate mulo de retorno uma programação directa que pode ser passado para um optimizador. A programação dá uma etapa como entrada e produz um valor calculado usando a fórmula CLR conforme apresentado no artigo.
steps_per_epoch = len(x_train) // BATCH_SIZE
clr = tfa.optimizers.CyclicalLearningRate(initial_learning_rate=INIT_LR,
maximal_learning_rate=MAX_LR,
scale_fn=lambda x: 1/(2.**(x-1)),
step_size=2 * steps_per_epoch
)
optimizer = tf.keras.optimizers.SGD(clr)
Aqui, você especifica os limites inferior e superior da taxa de aprendizagem e a programação irá oscilar entre esse intervalo ([1e-4, 1e-2], neste caso). scale_fn é usado para definir a função que iria aumentar e escalar para baixo a taxa de aprendizagem dentro de um determinado ciclo. step_size define a duração de um único ciclo. A step_size de 2 significa que você precisa de um total de 4 iterações para completar um ciclo. O valor recomendado para step_size é a seguinte:
factor * steps_per_epoch onde mentiras fatores dentro do intervalo [2, 8].
No mesmo papel CLR , Leslie também apresentou um método simples e elegante e escolher os limites de taxa de aprendizagem. Você é incentivado a verificar também. Este post fornece uma boa introdução ao método.
Abaixo, você visualizar como os clr olhares agenda como.
step = np.arange(0, EPOCHS * steps_per_epoch)
lr = clr(step)
plt.plot(step, lr)
plt.xlabel("Steps")
plt.ylabel("Learning Rate")
plt.show()
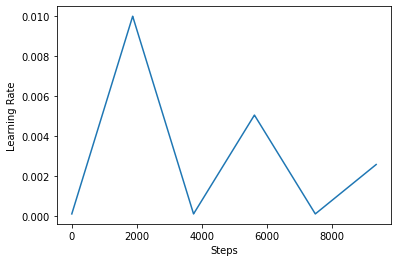
Para visualizar melhor o efeito do CLR, você pode traçar a programação com um número maior de etapas.
step = np.arange(0, 100 * steps_per_epoch)
lr = clr(step)
plt.plot(step, lr)
plt.xlabel("Steps")
plt.ylabel("Learning Rate")
plt.show()
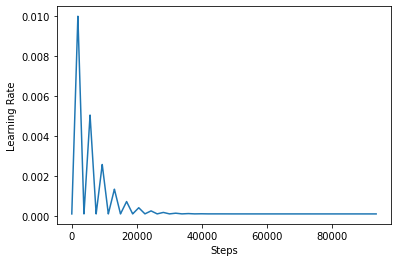
A função que você está usando neste tutorial é referido como o triangular2 método no papel CLR. Existem duas outras funções não foram exploradas nomeadamente triangular e exp (curto para exponencial).
Treine um modelo com CLR
clr_model = tf.keras.models.load_model("initial_model")
clr_history = train_model(clr_model, optimizer=optimizer)
WARNING:tensorflow:No training configuration found in save file, so the model was *not* compiled. Compile it manually. Epoch 1/10 938/938 [==============================] - 4s 4ms/step - loss: 2.3005 - accuracy: 0.1165 - val_loss: 2.2852 - val_accuracy: 0.2378 Epoch 2/10 938/938 [==============================] - 3s 4ms/step - loss: 2.1931 - accuracy: 0.2398 - val_loss: 1.7386 - val_accuracy: 0.4530 Epoch 3/10 938/938 [==============================] - 3s 4ms/step - loss: 1.3132 - accuracy: 0.5052 - val_loss: 1.0110 - val_accuracy: 0.6482 Epoch 4/10 938/938 [==============================] - 3s 4ms/step - loss: 1.0746 - accuracy: 0.5933 - val_loss: 0.9492 - val_accuracy: 0.6622 Epoch 5/10 938/938 [==============================] - 3s 4ms/step - loss: 1.0528 - accuracy: 0.6028 - val_loss: 0.9439 - val_accuracy: 0.6519 Epoch 6/10 938/938 [==============================] - 3s 4ms/step - loss: 1.0198 - accuracy: 0.6172 - val_loss: 0.9096 - val_accuracy: 0.6620 Epoch 7/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9778 - accuracy: 0.6339 - val_loss: 0.8784 - val_accuracy: 0.6746 Epoch 8/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9535 - accuracy: 0.6487 - val_loss: 0.8665 - val_accuracy: 0.6903 Epoch 9/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9510 - accuracy: 0.6497 - val_loss: 0.8691 - val_accuracy: 0.6857 Epoch 10/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9424 - accuracy: 0.6529 - val_loss: 0.8571 - val_accuracy: 0.6917
Como esperado, a perda começa mais alta do que o normal e então se estabiliza com o progresso do ciclo. Você pode confirmar isso visualmente com os gráficos abaixo.
Visualize perdas
(fig, ax) = plt.subplots(2, 1, figsize=(10, 8))
ax[0].plot(no_clr_history.history["loss"], label="train_loss")
ax[0].plot(no_clr_history.history["val_loss"], label="val_loss")
ax[0].set_title("No CLR")
ax[0].set_xlabel("Epochs")
ax[0].set_ylabel("Loss")
ax[0].set_ylim([0, 2.5])
ax[0].legend()
ax[1].plot(clr_history.history["loss"], label="train_loss")
ax[1].plot(clr_history.history["val_loss"], label="val_loss")
ax[1].set_title("CLR")
ax[1].set_xlabel("Epochs")
ax[1].set_ylabel("Loss")
ax[1].set_ylim([0, 2.5])
ax[1].legend()
fig.tight_layout(pad=3.0)
fig.show()
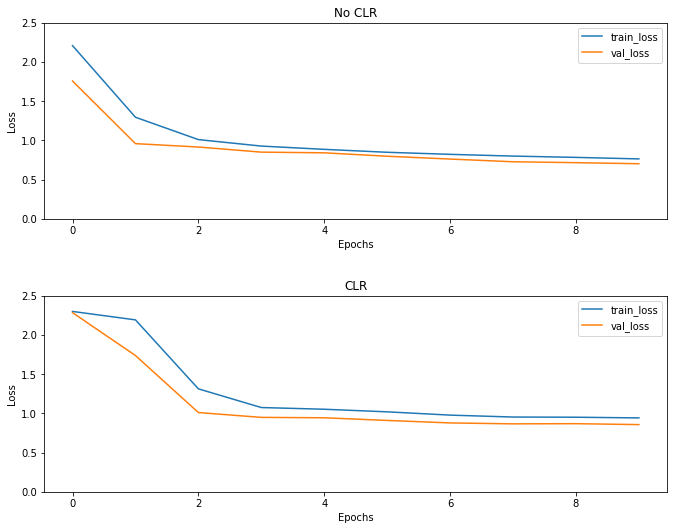
Mesmo que para este exemplo brinquedo, você não vê os efeitos da CLR muito, mas se notar que é um dos principais ingredientes atrás Super Convergência e pode ter um realmente bom impacto ao treinar em ambientes de larga escala.

