 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
Przegląd
Ten samouczek demonstruje użycie Cyclical Learning Rate z pakietu Addons.
Cykliczne wskaźniki uczenia się
Wykazano, że korzystne jest dostosowywanie tempa uczenia się w miarę postępu treningu dla sieci neuronowej. Ma wiele zalet, od odzyskiwania punktu siodła po zapobieganie niestabilności liczbowej, która może powstać podczas wstecznej propagacji. Ale skąd można wiedzieć, ile należy dostosować w odniesieniu do konkretnego znacznika czasu treningu? W 2015 r. Leslie Smith zauważył, że chciałbyś zwiększyć tempo uczenia się, aby szybciej przejść przez krajobraz strat, ale chciałbyś również zmniejszyć tempo uczenia się, gdy zbliżasz się do konwergencji. Aby zrealizować ten pomysł, zaproponował Cykliczne Learning ceny (CLR) gdzie byś dostosować szybkość uczenia się w odniesieniu do cykli funkcji. Dla wizualnej demonstracji, można sprawdzić ten blog . CLR jest teraz dostępny jako API TensorFlow. Aby uzyskać więcej informacji, zapoznaj się z oryginalnego papieru tutaj .
Ustawiać
pip install -q -U tensorflow_addons
from tensorflow.keras import layers
import tensorflow_addons as tfa
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
tf.random.set_seed(42)
np.random.seed(42)
Załaduj i przygotuj zbiór danych
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
x_train = np.expand_dims(x_train, -1)
x_test = np.expand_dims(x_test, -1)
Zdefiniuj hiperparametry
BATCH_SIZE = 64
EPOCHS = 10
INIT_LR = 1e-4
MAX_LR = 1e-2
Zdefiniuj narzędzia do budowania modeli i uczenia modeli
def get_training_model():
model = tf.keras.Sequential(
[
layers.InputLayer((28, 28, 1)),
layers.experimental.preprocessing.Rescaling(scale=1./255),
layers.Conv2D(16, (5, 5), activation="relu"),
layers.MaxPooling2D(pool_size=(2, 2)),
layers.Conv2D(32, (5, 5), activation="relu"),
layers.MaxPooling2D(pool_size=(2, 2)),
layers.SpatialDropout2D(0.2),
layers.GlobalAvgPool2D(),
layers.Dense(128, activation="relu"),
layers.Dense(10, activation="softmax"),
]
)
return model
def train_model(model, optimizer):
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer,
metrics=["accuracy"])
history = model.fit(x_train,
y_train,
batch_size=BATCH_SIZE,
validation_data=(x_test, y_test),
epochs=EPOCHS)
return history
W interesie odtwarzalności, początkowe wagi modeli są szeregowane, których będziesz używać do przeprowadzania naszych eksperymentów.
initial_model = get_training_model()
initial_model.save("initial_model")
WARNING:tensorflow:Compiled the loaded model, but the compiled metrics have yet to be built. `model.compile_metrics` will be empty until you train or evaluate the model. 2021-11-12 19:14:52.355642: W tensorflow/python/util/util.cc:368] Sets are not currently considered sequences, but this may change in the future, so consider avoiding using them. INFO:tensorflow:Assets written to: initial_model/assets
Trenuj model bez CLR
standard_model = tf.keras.models.load_model("initial_model")
no_clr_history = train_model(standard_model, optimizer="sgd")
WARNING:tensorflow:No training configuration found in save file, so the model was *not* compiled. Compile it manually. Epoch 1/10 938/938 [==============================] - 5s 4ms/step - loss: 2.2089 - accuracy: 0.2180 - val_loss: 1.7581 - val_accuracy: 0.4137 Epoch 2/10 938/938 [==============================] - 3s 3ms/step - loss: 1.2951 - accuracy: 0.5136 - val_loss: 0.9583 - val_accuracy: 0.6491 Epoch 3/10 938/938 [==============================] - 3s 3ms/step - loss: 1.0096 - accuracy: 0.6189 - val_loss: 0.9155 - val_accuracy: 0.6588 Epoch 4/10 938/938 [==============================] - 3s 3ms/step - loss: 0.9269 - accuracy: 0.6572 - val_loss: 0.8495 - val_accuracy: 0.7011 Epoch 5/10 938/938 [==============================] - 3s 3ms/step - loss: 0.8855 - accuracy: 0.6722 - val_loss: 0.8361 - val_accuracy: 0.6685 Epoch 6/10 938/938 [==============================] - 3s 3ms/step - loss: 0.8482 - accuracy: 0.6852 - val_loss: 0.7975 - val_accuracy: 0.6830 Epoch 7/10 938/938 [==============================] - 3s 3ms/step - loss: 0.8219 - accuracy: 0.6941 - val_loss: 0.7630 - val_accuracy: 0.6990 Epoch 8/10 938/938 [==============================] - 3s 3ms/step - loss: 0.7995 - accuracy: 0.7011 - val_loss: 0.7280 - val_accuracy: 0.7263 Epoch 9/10 938/938 [==============================] - 3s 3ms/step - loss: 0.7830 - accuracy: 0.7059 - val_loss: 0.7156 - val_accuracy: 0.7445 Epoch 10/10 938/938 [==============================] - 3s 3ms/step - loss: 0.7636 - accuracy: 0.7136 - val_loss: 0.7026 - val_accuracy: 0.7462
Zdefiniuj harmonogram CLR
tfa.optimizers.CyclicalLearningRate moduł powrót bezpośrednio harmonogram, który może być przekazywany do Optimizer. Harmonogram przyjmuje krok jako dane wejściowe i wyprowadza wartość obliczoną za pomocą formuły CLR, jak przedstawiono w artykule.
steps_per_epoch = len(x_train) // BATCH_SIZE
clr = tfa.optimizers.CyclicalLearningRate(initial_learning_rate=INIT_LR,
maximal_learning_rate=MAX_LR,
scale_fn=lambda x: 1/(2.**(x-1)),
step_size=2 * steps_per_epoch
)
optimizer = tf.keras.optimizers.SGD(clr)
Tutaj należy określić górne i dolne granice szybkości uczenia się i harmonogram będzie oscylować pomiędzy tym zakresie ([1e-4, 1e-2] w tym przypadku). scale_fn służy do określenia funkcji, która skaluje się i zmniejszania szybkości uczenia się w danym cyklu. step_size określa czas trwania pojedynczego cyklu. step_size 2 oznacza, że trzeba w sumie 4 iteracjach, aby zakończyć jeden cykl. Zalecana wartość dla step_size przedstawia się następująco:
factor * steps_per_epoch gdzie leży czynnik w [2, 8] zakresu.
W tym samym papierze CLR , Leslie przedstawiła również prosty i elegancki sposób wybrać granice dla szybkości uczenia się. Zachęcamy również do sprawdzenia tego. Ten blogu zapewnia miły wprowadzenie do metody.
Poniżej wizualizować jak clr wygląda rozkład podoba.
step = np.arange(0, EPOCHS * steps_per_epoch)
lr = clr(step)
plt.plot(step, lr)
plt.xlabel("Steps")
plt.ylabel("Learning Rate")
plt.show()
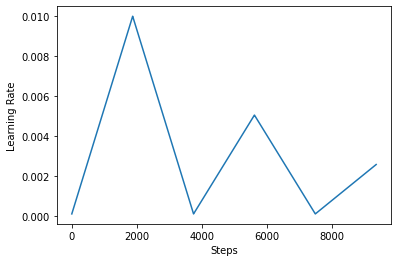
Aby lepiej zwizualizować efekt CLR, możesz wykreślić harmonogram ze zwiększoną liczbą kroków.
step = np.arange(0, 100 * steps_per_epoch)
lr = clr(step)
plt.plot(step, lr)
plt.xlabel("Steps")
plt.ylabel("Learning Rate")
plt.show()
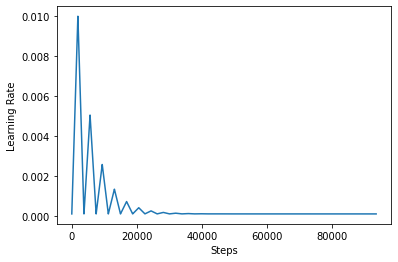
Funkcja używasz w tym kursie jest dalej triangular2 metody w papierze CLR. Istnieją inne dwie funkcje nie zostały zbadane mianowicie triangular i exp (skrót wykładniczą).
Trenuj model z CLR
clr_model = tf.keras.models.load_model("initial_model")
clr_history = train_model(clr_model, optimizer=optimizer)
WARNING:tensorflow:No training configuration found in save file, so the model was *not* compiled. Compile it manually. Epoch 1/10 938/938 [==============================] - 4s 4ms/step - loss: 2.3005 - accuracy: 0.1165 - val_loss: 2.2852 - val_accuracy: 0.2378 Epoch 2/10 938/938 [==============================] - 3s 4ms/step - loss: 2.1931 - accuracy: 0.2398 - val_loss: 1.7386 - val_accuracy: 0.4530 Epoch 3/10 938/938 [==============================] - 3s 4ms/step - loss: 1.3132 - accuracy: 0.5052 - val_loss: 1.0110 - val_accuracy: 0.6482 Epoch 4/10 938/938 [==============================] - 3s 4ms/step - loss: 1.0746 - accuracy: 0.5933 - val_loss: 0.9492 - val_accuracy: 0.6622 Epoch 5/10 938/938 [==============================] - 3s 4ms/step - loss: 1.0528 - accuracy: 0.6028 - val_loss: 0.9439 - val_accuracy: 0.6519 Epoch 6/10 938/938 [==============================] - 3s 4ms/step - loss: 1.0198 - accuracy: 0.6172 - val_loss: 0.9096 - val_accuracy: 0.6620 Epoch 7/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9778 - accuracy: 0.6339 - val_loss: 0.8784 - val_accuracy: 0.6746 Epoch 8/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9535 - accuracy: 0.6487 - val_loss: 0.8665 - val_accuracy: 0.6903 Epoch 9/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9510 - accuracy: 0.6497 - val_loss: 0.8691 - val_accuracy: 0.6857 Epoch 10/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9424 - accuracy: 0.6529 - val_loss: 0.8571 - val_accuracy: 0.6917
Zgodnie z oczekiwaniami strata zaczyna się wyższa niż zwykle, a następnie stabilizuje się wraz z postępem cykli. Możesz to potwierdzić wizualnie na poniższych wykresach.
Wizualizuj straty
(fig, ax) = plt.subplots(2, 1, figsize=(10, 8))
ax[0].plot(no_clr_history.history["loss"], label="train_loss")
ax[0].plot(no_clr_history.history["val_loss"], label="val_loss")
ax[0].set_title("No CLR")
ax[0].set_xlabel("Epochs")
ax[0].set_ylabel("Loss")
ax[0].set_ylim([0, 2.5])
ax[0].legend()
ax[1].plot(clr_history.history["loss"], label="train_loss")
ax[1].plot(clr_history.history["val_loss"], label="val_loss")
ax[1].set_title("CLR")
ax[1].set_xlabel("Epochs")
ax[1].set_ylabel("Loss")
ax[1].set_ylim([0, 2.5])
ax[1].legend()
fig.tight_layout(pad=3.0)
fig.show()
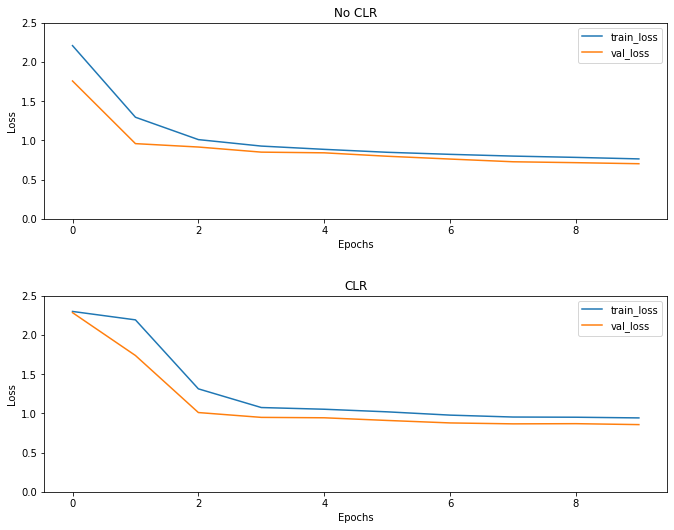
Chociaż w tym przykładzie zabawek, nie widział skutków CLR dużo, ale należy zauważyć, że jest to jeden z głównych składników za Super Konwergencja i może mieć bardzo dobry wpływ podczas treningu w ustawieniach na dużą skalę.

