 TensorFlow.org पर देखें TensorFlow.org पर देखें |  Google Colab में चलाएं Google Colab में चलाएं |  GitHub पर स्रोत देखें GitHub पर स्रोत देखें |  नोटबुक डाउनलोड करें नोटबुक डाउनलोड करें |
अवलोकन
यह ट्यूटोरियल एडॉन्स पैकेज से चक्रीय सीखने की दर के उपयोग को दर्शाता है।
चक्रीय सीखने की दरें
यह दिखाया गया है कि तंत्रिका नेटवर्क के लिए प्रशिक्षण की प्रगति के रूप में सीखने की दर को समायोजित करना फायदेमंद है। बैकप्रॉपैगेशन के दौरान उत्पन्न होने वाली संख्यात्मक अस्थिरताओं को रोकने के लिए सैडल पॉइंट रिकवरी से लेकर इसके कई गुना लाभ हैं। लेकिन कोई कैसे जानता है कि किसी विशेष प्रशिक्षण टाइमस्टैम्प के संबंध में कितना समायोजन करना है? 2015 में, लेस्ली स्मिथ ने देखा कि आप हानि परिदृश्य में तेजी से आगे बढ़ने के लिए सीखने की दर में वृद्धि करना चाहते हैं, लेकिन अभिसरण के करीब पहुंचने पर आप सीखने की दर को भी कम करना चाहेंगे। इस विचार को साकार करने के लिए उन्होंने प्रस्ताव किया चक्रीय लर्निंग दरें (CLR) जहाँ आप एक समारोह के चक्र के संबंध में सीखने दर को समायोजित करेगा। एक दृश्य प्रदर्शन के लिए, आप देख सकते हैं इस ब्लॉग । CLR अब TensorFlow API के रूप में उपलब्ध है। अधिक जानकारी के लिए मूल शोध-पत्र की जाँच यहां ।
सेट अप
pip install -q -U tensorflow_addons
from tensorflow.keras import layers
import tensorflow_addons as tfa
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
tf.random.set_seed(42)
np.random.seed(42)
डेटासेट लोड करें और तैयार करें
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
x_train = np.expand_dims(x_train, -1)
x_test = np.expand_dims(x_test, -1)
हाइपरपैरामीटर को परिभाषित करें
BATCH_SIZE = 64
EPOCHS = 10
INIT_LR = 1e-4
MAX_LR = 1e-2
मॉडल निर्माण और मॉडल प्रशिक्षण उपयोगिताओं को परिभाषित करें
def get_training_model():
model = tf.keras.Sequential(
[
layers.InputLayer((28, 28, 1)),
layers.experimental.preprocessing.Rescaling(scale=1./255),
layers.Conv2D(16, (5, 5), activation="relu"),
layers.MaxPooling2D(pool_size=(2, 2)),
layers.Conv2D(32, (5, 5), activation="relu"),
layers.MaxPooling2D(pool_size=(2, 2)),
layers.SpatialDropout2D(0.2),
layers.GlobalAvgPool2D(),
layers.Dense(128, activation="relu"),
layers.Dense(10, activation="softmax"),
]
)
return model
def train_model(model, optimizer):
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer,
metrics=["accuracy"])
history = model.fit(x_train,
y_train,
batch_size=BATCH_SIZE,
validation_data=(x_test, y_test),
epochs=EPOCHS)
return history
प्रतिलिपि प्रस्तुत करने योग्यता के हित में, प्रारंभिक मॉडल भारों को क्रमबद्ध किया जाता है जिसका उपयोग आप हमारे प्रयोग करने के लिए करेंगे।
initial_model = get_training_model()
initial_model.save("initial_model")
WARNING:tensorflow:Compiled the loaded model, but the compiled metrics have yet to be built. `model.compile_metrics` will be empty until you train or evaluate the model. 2021-11-12 19:14:52.355642: W tensorflow/python/util/util.cc:368] Sets are not currently considered sequences, but this may change in the future, so consider avoiding using them. INFO:tensorflow:Assets written to: initial_model/assets
सीएलआर के बिना एक मॉडल को प्रशिक्षित करें
standard_model = tf.keras.models.load_model("initial_model")
no_clr_history = train_model(standard_model, optimizer="sgd")
WARNING:tensorflow:No training configuration found in save file, so the model was *not* compiled. Compile it manually. Epoch 1/10 938/938 [==============================] - 5s 4ms/step - loss: 2.2089 - accuracy: 0.2180 - val_loss: 1.7581 - val_accuracy: 0.4137 Epoch 2/10 938/938 [==============================] - 3s 3ms/step - loss: 1.2951 - accuracy: 0.5136 - val_loss: 0.9583 - val_accuracy: 0.6491 Epoch 3/10 938/938 [==============================] - 3s 3ms/step - loss: 1.0096 - accuracy: 0.6189 - val_loss: 0.9155 - val_accuracy: 0.6588 Epoch 4/10 938/938 [==============================] - 3s 3ms/step - loss: 0.9269 - accuracy: 0.6572 - val_loss: 0.8495 - val_accuracy: 0.7011 Epoch 5/10 938/938 [==============================] - 3s 3ms/step - loss: 0.8855 - accuracy: 0.6722 - val_loss: 0.8361 - val_accuracy: 0.6685 Epoch 6/10 938/938 [==============================] - 3s 3ms/step - loss: 0.8482 - accuracy: 0.6852 - val_loss: 0.7975 - val_accuracy: 0.6830 Epoch 7/10 938/938 [==============================] - 3s 3ms/step - loss: 0.8219 - accuracy: 0.6941 - val_loss: 0.7630 - val_accuracy: 0.6990 Epoch 8/10 938/938 [==============================] - 3s 3ms/step - loss: 0.7995 - accuracy: 0.7011 - val_loss: 0.7280 - val_accuracy: 0.7263 Epoch 9/10 938/938 [==============================] - 3s 3ms/step - loss: 0.7830 - accuracy: 0.7059 - val_loss: 0.7156 - val_accuracy: 0.7445 Epoch 10/10 938/938 [==============================] - 3s 3ms/step - loss: 0.7636 - accuracy: 0.7136 - val_loss: 0.7026 - val_accuracy: 0.7462
सीएलआर शेड्यूल को परिभाषित करें
tfa.optimizers.CyclicalLearningRate एक सीधा अनुसूची एक अनुकूलक करने के लिए पारित किया जा सकता है कि वापसी मॉड्यूल। शेड्यूल अपने इनपुट के रूप में एक कदम उठाता है और पेपर में निर्धारित सीएलआर फॉर्मूला का उपयोग करके गणना किए गए मूल्य को आउटपुट करता है।
steps_per_epoch = len(x_train) // BATCH_SIZE
clr = tfa.optimizers.CyclicalLearningRate(initial_learning_rate=INIT_LR,
maximal_learning_rate=MAX_LR,
scale_fn=lambda x: 1/(2.**(x-1)),
step_size=2 * steps_per_epoch
)
optimizer = tf.keras.optimizers.SGD(clr)
यहाँ, आप सीखने दर के निचले और ऊपरी सीमा निर्दिष्ट और अनुसूची कि सीमा के बीच में दोलन होगा ([1e-4, 1e-2] इस मामले में)। scale_fn समारोह है कि पैमाने और किसी दिए गए चक्र के भीतर सीखने दर नीचे पैमाने पर होगा परिभाषित करने के लिए प्रयोग किया जाता है। step_size एक एकल चक्र की अवधि परिभाषित करता है। एक step_size 2 का मतलब है की आप एक चक्र पूरा करने के लिए 4 पुनरावृत्तियों की कुल जरूरत है। के लिए सिफारिश की मूल्य step_size इस प्रकार है:
factor * steps_per_epoch जहां [2, 8] सीमा के भीतर कारक निहित है।
एक ही में CLR कागज , लेस्ली भी दर सीखने के लिए सीमा का चयन करने के लिए एक सरल और सुरुचिपूर्ण विधि प्रस्तुत किया। आपको इसे भी जांचने के लिए प्रोत्साहित किया जाता है। इस ब्लॉग पोस्ट विधि के लिए एक अच्छा परिचय प्रदान करता है।
नीचे, आप कल्पना कैसे clr अनुसूची लगता है।
step = np.arange(0, EPOCHS * steps_per_epoch)
lr = clr(step)
plt.plot(step, lr)
plt.xlabel("Steps")
plt.ylabel("Learning Rate")
plt.show()
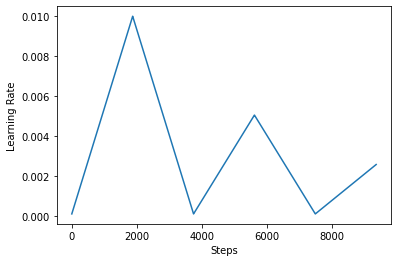
सीएलआर के प्रभाव को बेहतर ढंग से देखने के लिए, आप अधिक चरणों के साथ शेड्यूल तैयार कर सकते हैं।
step = np.arange(0, 100 * steps_per_epoch)
lr = clr(step)
plt.plot(step, lr)
plt.xlabel("Steps")
plt.ylabel("Learning Rate")
plt.show()
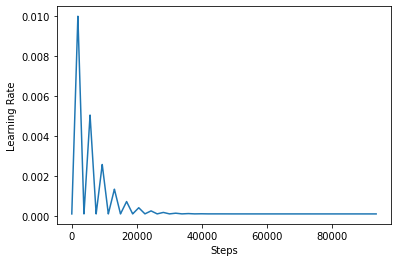
समारोह आप इस ट्यूटोरियल में प्रयोग कर रहे हैं के रूप में जाना जाता है triangular2 CLR पत्र में विधि। वहाँ अन्य दो कार्य अर्थात् वहाँ का पता लगाया गया हैं triangular और exp (लघु घातीय के लिए)।
CLR . के साथ एक मॉडल को प्रशिक्षित करें
clr_model = tf.keras.models.load_model("initial_model")
clr_history = train_model(clr_model, optimizer=optimizer)
WARNING:tensorflow:No training configuration found in save file, so the model was *not* compiled. Compile it manually. Epoch 1/10 938/938 [==============================] - 4s 4ms/step - loss: 2.3005 - accuracy: 0.1165 - val_loss: 2.2852 - val_accuracy: 0.2378 Epoch 2/10 938/938 [==============================] - 3s 4ms/step - loss: 2.1931 - accuracy: 0.2398 - val_loss: 1.7386 - val_accuracy: 0.4530 Epoch 3/10 938/938 [==============================] - 3s 4ms/step - loss: 1.3132 - accuracy: 0.5052 - val_loss: 1.0110 - val_accuracy: 0.6482 Epoch 4/10 938/938 [==============================] - 3s 4ms/step - loss: 1.0746 - accuracy: 0.5933 - val_loss: 0.9492 - val_accuracy: 0.6622 Epoch 5/10 938/938 [==============================] - 3s 4ms/step - loss: 1.0528 - accuracy: 0.6028 - val_loss: 0.9439 - val_accuracy: 0.6519 Epoch 6/10 938/938 [==============================] - 3s 4ms/step - loss: 1.0198 - accuracy: 0.6172 - val_loss: 0.9096 - val_accuracy: 0.6620 Epoch 7/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9778 - accuracy: 0.6339 - val_loss: 0.8784 - val_accuracy: 0.6746 Epoch 8/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9535 - accuracy: 0.6487 - val_loss: 0.8665 - val_accuracy: 0.6903 Epoch 9/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9510 - accuracy: 0.6497 - val_loss: 0.8691 - val_accuracy: 0.6857 Epoch 10/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9424 - accuracy: 0.6529 - val_loss: 0.8571 - val_accuracy: 0.6917
जैसा कि अपेक्षित था नुकसान सामान्य से अधिक शुरू होता है और फिर चक्र की प्रगति के रूप में यह स्थिर हो जाता है। आप नीचे दिए गए भूखंडों के साथ नेत्रहीन इसकी पुष्टि कर सकते हैं।
नुकसान की कल्पना करें
(fig, ax) = plt.subplots(2, 1, figsize=(10, 8))
ax[0].plot(no_clr_history.history["loss"], label="train_loss")
ax[0].plot(no_clr_history.history["val_loss"], label="val_loss")
ax[0].set_title("No CLR")
ax[0].set_xlabel("Epochs")
ax[0].set_ylabel("Loss")
ax[0].set_ylim([0, 2.5])
ax[0].legend()
ax[1].plot(clr_history.history["loss"], label="train_loss")
ax[1].plot(clr_history.history["val_loss"], label="val_loss")
ax[1].set_title("CLR")
ax[1].set_xlabel("Epochs")
ax[1].set_ylabel("Loss")
ax[1].set_ylim([0, 2.5])
ax[1].legend()
fig.tight_layout(pad=3.0)
fig.show()
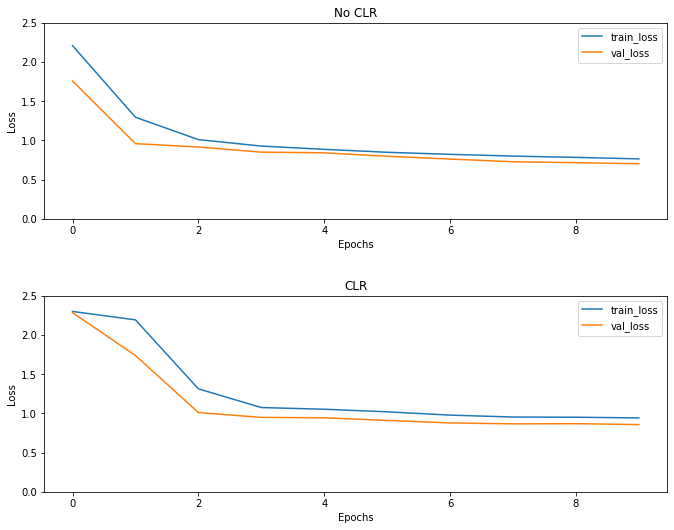
हालांकि इस खिलौने उदाहरण के लिए, आप CLR का प्रभाव ज्यादा नहीं देखा लेकिन ध्यान दिया जाना है कि इसके पीछे मुख्य तत्व में से एक है सुपर कन्वर्जेंस और एक हो सकता है वास्तव में अच्छा प्रभाव जब बड़े पैमाने पर सेटिंग्स में प्रशिक्षण।

