 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Aperçu
Ce didacticiel montre l'utilisation du taux d'apprentissage cyclique du package Addons.
Taux d'apprentissage cyclique
Il a été démontré qu'il est bénéfique d'ajuster le taux d'apprentissage au fur et à mesure que la formation progresse pour un réseau de neurones. Il présente de nombreux avantages, allant de la récupération du point de selle à la prévention des instabilités numériques pouvant survenir lors de la rétropropagation. Mais comment savoir combien ajuster par rapport à un horodatage d'entraînement particulier ? En 2015, Leslie Smith a remarqué que vous voudriez augmenter le taux d'apprentissage pour parcourir plus rapidement le paysage des pertes, mais que vous voudriez également réduire le taux d'apprentissage à l'approche de la convergence. Pour réaliser cette idée, il a proposé Cyclique apprentissage Tarifs (CLR) où vous réglez le taux d' apprentissage par rapport aux cycles d'une fonction. Pour une démonstration visuelle, vous pouvez consulter ce blog . CLR est désormais disponible en tant qu'API TensorFlow. Pour plus de détails, consultez l'article original ici .
Installer
pip install -q -U tensorflow_addons
from tensorflow.keras import layers
import tensorflow_addons as tfa
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
tf.random.set_seed(42)
np.random.seed(42)
Charger et préparer l'ensemble de données
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
x_train = np.expand_dims(x_train, -1)
x_test = np.expand_dims(x_test, -1)
Définir des hyperparamètres
BATCH_SIZE = 64
EPOCHS = 10
INIT_LR = 1e-4
MAX_LR = 1e-2
Définir les utilitaires de création de modèles et de formation de modèles
def get_training_model():
model = tf.keras.Sequential(
[
layers.InputLayer((28, 28, 1)),
layers.experimental.preprocessing.Rescaling(scale=1./255),
layers.Conv2D(16, (5, 5), activation="relu"),
layers.MaxPooling2D(pool_size=(2, 2)),
layers.Conv2D(32, (5, 5), activation="relu"),
layers.MaxPooling2D(pool_size=(2, 2)),
layers.SpatialDropout2D(0.2),
layers.GlobalAvgPool2D(),
layers.Dense(128, activation="relu"),
layers.Dense(10, activation="softmax"),
]
)
return model
def train_model(model, optimizer):
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer,
metrics=["accuracy"])
history = model.fit(x_train,
y_train,
batch_size=BATCH_SIZE,
validation_data=(x_test, y_test),
epochs=EPOCHS)
return history
Dans l'intérêt de la reproductibilité, les poids initiaux du modèle sont sérialisés que vous utiliserez pour mener nos expériences.
initial_model = get_training_model()
initial_model.save("initial_model")
WARNING:tensorflow:Compiled the loaded model, but the compiled metrics have yet to be built. `model.compile_metrics` will be empty until you train or evaluate the model. 2021-11-12 19:14:52.355642: W tensorflow/python/util/util.cc:368] Sets are not currently considered sequences, but this may change in the future, so consider avoiding using them. INFO:tensorflow:Assets written to: initial_model/assets
Former un modèle sans CLR
standard_model = tf.keras.models.load_model("initial_model")
no_clr_history = train_model(standard_model, optimizer="sgd")
WARNING:tensorflow:No training configuration found in save file, so the model was *not* compiled. Compile it manually. Epoch 1/10 938/938 [==============================] - 5s 4ms/step - loss: 2.2089 - accuracy: 0.2180 - val_loss: 1.7581 - val_accuracy: 0.4137 Epoch 2/10 938/938 [==============================] - 3s 3ms/step - loss: 1.2951 - accuracy: 0.5136 - val_loss: 0.9583 - val_accuracy: 0.6491 Epoch 3/10 938/938 [==============================] - 3s 3ms/step - loss: 1.0096 - accuracy: 0.6189 - val_loss: 0.9155 - val_accuracy: 0.6588 Epoch 4/10 938/938 [==============================] - 3s 3ms/step - loss: 0.9269 - accuracy: 0.6572 - val_loss: 0.8495 - val_accuracy: 0.7011 Epoch 5/10 938/938 [==============================] - 3s 3ms/step - loss: 0.8855 - accuracy: 0.6722 - val_loss: 0.8361 - val_accuracy: 0.6685 Epoch 6/10 938/938 [==============================] - 3s 3ms/step - loss: 0.8482 - accuracy: 0.6852 - val_loss: 0.7975 - val_accuracy: 0.6830 Epoch 7/10 938/938 [==============================] - 3s 3ms/step - loss: 0.8219 - accuracy: 0.6941 - val_loss: 0.7630 - val_accuracy: 0.6990 Epoch 8/10 938/938 [==============================] - 3s 3ms/step - loss: 0.7995 - accuracy: 0.7011 - val_loss: 0.7280 - val_accuracy: 0.7263 Epoch 9/10 938/938 [==============================] - 3s 3ms/step - loss: 0.7830 - accuracy: 0.7059 - val_loss: 0.7156 - val_accuracy: 0.7445 Epoch 10/10 938/938 [==============================] - 3s 3ms/step - loss: 0.7636 - accuracy: 0.7136 - val_loss: 0.7026 - val_accuracy: 0.7462
Définir le calendrier CLR
Le tfa.optimizers.CyclicalLearningRate module retourne un programme direct qui peut être transmis à un optimiseur. Le calendrier prend une étape en tant qu'entrée et génère une valeur calculée à l'aide de la formule CLR telle qu'elle est présentée dans le document.
steps_per_epoch = len(x_train) // BATCH_SIZE
clr = tfa.optimizers.CyclicalLearningRate(initial_learning_rate=INIT_LR,
maximal_learning_rate=MAX_LR,
scale_fn=lambda x: 1/(2.**(x-1)),
step_size=2 * steps_per_epoch
)
optimizer = tf.keras.optimizers.SGD(clr)
Ici, vous spécifiez les bornes inférieures et supérieures du taux d'apprentissage et le calendrier oscillera entre cette plage ([1E-4, 1E-2] dans ce cas). scale_fn permet de définir la fonction qui l' échelle et réduire le taux d'apprentissage dans un cycle donné. step_size définit la durée d'un seul cycle. Un step_size de 2 signifie que vous avez besoin d' un total de 4 itérations à cycle complet d'un. La valeur recommandée pour step_size est la suivante:
factor * steps_per_epoch où le facteur se situe dans le [2, 8] gamme.
Dans le même papier CLR , Leslie a également présenté une méthode simple et élégante de choisir les limites pour le taux d' apprentissage. Vous êtes également encouragé à le vérifier. Ce billet de blog fournit une bonne introduction à la méthode.
Ci - dessous, vous visualisez comment les clr calendrier ressemble.
step = np.arange(0, EPOCHS * steps_per_epoch)
lr = clr(step)
plt.plot(step, lr)
plt.xlabel("Steps")
plt.ylabel("Learning Rate")
plt.show()
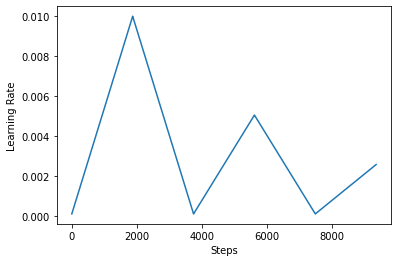
Afin de mieux visualiser l'effet du CLR, vous pouvez tracer le calendrier avec un nombre accru d'étapes.
step = np.arange(0, 100 * steps_per_epoch)
lr = clr(step)
plt.plot(step, lr)
plt.xlabel("Steps")
plt.ylabel("Learning Rate")
plt.show()
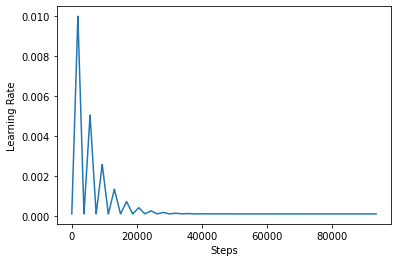
La fonction que vous utilisez dans ce tutoriel est appelée triangular2 méthode dans le papier CLR. Il y a deux autres fonctions , il ont été explorées à savoir triangular et exp (abréviation exponentielle).
Former un modèle avec CLR
clr_model = tf.keras.models.load_model("initial_model")
clr_history = train_model(clr_model, optimizer=optimizer)
WARNING:tensorflow:No training configuration found in save file, so the model was *not* compiled. Compile it manually. Epoch 1/10 938/938 [==============================] - 4s 4ms/step - loss: 2.3005 - accuracy: 0.1165 - val_loss: 2.2852 - val_accuracy: 0.2378 Epoch 2/10 938/938 [==============================] - 3s 4ms/step - loss: 2.1931 - accuracy: 0.2398 - val_loss: 1.7386 - val_accuracy: 0.4530 Epoch 3/10 938/938 [==============================] - 3s 4ms/step - loss: 1.3132 - accuracy: 0.5052 - val_loss: 1.0110 - val_accuracy: 0.6482 Epoch 4/10 938/938 [==============================] - 3s 4ms/step - loss: 1.0746 - accuracy: 0.5933 - val_loss: 0.9492 - val_accuracy: 0.6622 Epoch 5/10 938/938 [==============================] - 3s 4ms/step - loss: 1.0528 - accuracy: 0.6028 - val_loss: 0.9439 - val_accuracy: 0.6519 Epoch 6/10 938/938 [==============================] - 3s 4ms/step - loss: 1.0198 - accuracy: 0.6172 - val_loss: 0.9096 - val_accuracy: 0.6620 Epoch 7/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9778 - accuracy: 0.6339 - val_loss: 0.8784 - val_accuracy: 0.6746 Epoch 8/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9535 - accuracy: 0.6487 - val_loss: 0.8665 - val_accuracy: 0.6903 Epoch 9/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9510 - accuracy: 0.6497 - val_loss: 0.8691 - val_accuracy: 0.6857 Epoch 10/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9424 - accuracy: 0.6529 - val_loss: 0.8571 - val_accuracy: 0.6917
Comme prévu, la perte commence plus haut que d'habitude, puis elle se stabilise au fur et à mesure que les cycles progressent. Vous pouvez le confirmer visuellement avec les graphiques ci-dessous.
Visualisez les pertes
(fig, ax) = plt.subplots(2, 1, figsize=(10, 8))
ax[0].plot(no_clr_history.history["loss"], label="train_loss")
ax[0].plot(no_clr_history.history["val_loss"], label="val_loss")
ax[0].set_title("No CLR")
ax[0].set_xlabel("Epochs")
ax[0].set_ylabel("Loss")
ax[0].set_ylim([0, 2.5])
ax[0].legend()
ax[1].plot(clr_history.history["loss"], label="train_loss")
ax[1].plot(clr_history.history["val_loss"], label="val_loss")
ax[1].set_title("CLR")
ax[1].set_xlabel("Epochs")
ax[1].set_ylabel("Loss")
ax[1].set_ylim([0, 2.5])
ax[1].legend()
fig.tight_layout(pad=3.0)
fig.show()
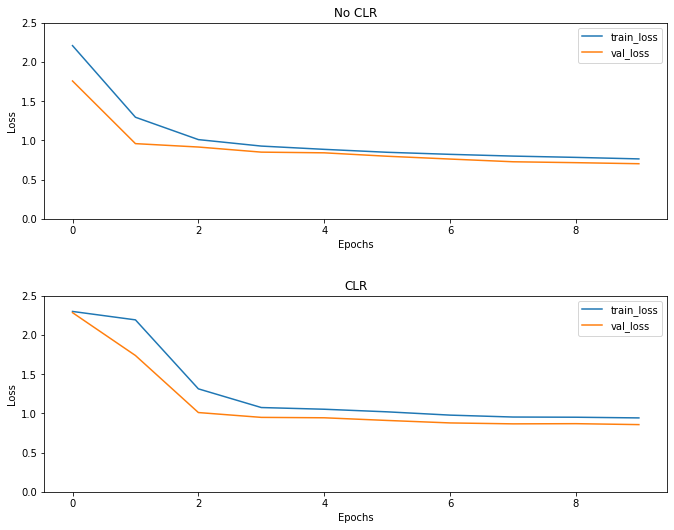
Même si cet exemple de jouet, vous ne voyez pas les effets du CLR beaucoup , mais noter qu'il est l' un des principaux ingrédients derrière super convergence et peut avoir un effet très bon lors de la formation dans les milieux à grande échelle.

