 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar cuaderno Descargar cuaderno |
Visión general
Este tutorial demuestra el uso de Cyclical Learning Rate del paquete Addons.
Tasas de aprendizaje cíclico
Se ha demostrado que es beneficioso ajustar la tasa de aprendizaje a medida que avanza el entrenamiento para una red neuronal. Tiene múltiples beneficios que van desde la recuperación del punto silla hasta la prevención de inestabilidades numéricas que pueden surgir durante la propagación hacia atrás. Pero, ¿cómo se sabe cuánto ajustar con respecto a una marca de tiempo de entrenamiento en particular? En 2015, Leslie Smith notó que querría aumentar la tasa de aprendizaje para atravesar más rápido el panorama de pérdidas, pero también querría reducir la tasa de aprendizaje al acercarse a la convergencia. Para llevar a cabo esta idea, propuso cíclico de aprendizaje Precios (CLR) donde desea ajustar la tasa de aprendizaje con respecto a los ciclos de una función. Para una demostración visual, usted puede sacar de este blog . CLR ahora está disponible como una API de TensorFlow. Para más detalles, ver el artículo original aquí .
Configuración
pip install -q -U tensorflow_addons
from tensorflow.keras import layers
import tensorflow_addons as tfa
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
tf.random.set_seed(42)
np.random.seed(42)
Cargar y preparar el conjunto de datos
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
x_train = np.expand_dims(x_train, -1)
x_test = np.expand_dims(x_test, -1)
Definir hiperparámetros
BATCH_SIZE = 64
EPOCHS = 10
INIT_LR = 1e-4
MAX_LR = 1e-2
Definir la construcción de modelos y las utilidades de entrenamiento de modelos.
def get_training_model():
model = tf.keras.Sequential(
[
layers.InputLayer((28, 28, 1)),
layers.experimental.preprocessing.Rescaling(scale=1./255),
layers.Conv2D(16, (5, 5), activation="relu"),
layers.MaxPooling2D(pool_size=(2, 2)),
layers.Conv2D(32, (5, 5), activation="relu"),
layers.MaxPooling2D(pool_size=(2, 2)),
layers.SpatialDropout2D(0.2),
layers.GlobalAvgPool2D(),
layers.Dense(128, activation="relu"),
layers.Dense(10, activation="softmax"),
]
)
return model
def train_model(model, optimizer):
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer,
metrics=["accuracy"])
history = model.fit(x_train,
y_train,
batch_size=BATCH_SIZE,
validation_data=(x_test, y_test),
epochs=EPOCHS)
return history
En aras de la reproducibilidad, se serializan los pesos del modelo inicial que utilizará para realizar nuestros experimentos.
initial_model = get_training_model()
initial_model.save("initial_model")
WARNING:tensorflow:Compiled the loaded model, but the compiled metrics have yet to be built. `model.compile_metrics` will be empty until you train or evaluate the model. 2021-11-12 19:14:52.355642: W tensorflow/python/util/util.cc:368] Sets are not currently considered sequences, but this may change in the future, so consider avoiding using them. INFO:tensorflow:Assets written to: initial_model/assets
Entrene un modelo sin CLR
standard_model = tf.keras.models.load_model("initial_model")
no_clr_history = train_model(standard_model, optimizer="sgd")
WARNING:tensorflow:No training configuration found in save file, so the model was *not* compiled. Compile it manually. Epoch 1/10 938/938 [==============================] - 5s 4ms/step - loss: 2.2089 - accuracy: 0.2180 - val_loss: 1.7581 - val_accuracy: 0.4137 Epoch 2/10 938/938 [==============================] - 3s 3ms/step - loss: 1.2951 - accuracy: 0.5136 - val_loss: 0.9583 - val_accuracy: 0.6491 Epoch 3/10 938/938 [==============================] - 3s 3ms/step - loss: 1.0096 - accuracy: 0.6189 - val_loss: 0.9155 - val_accuracy: 0.6588 Epoch 4/10 938/938 [==============================] - 3s 3ms/step - loss: 0.9269 - accuracy: 0.6572 - val_loss: 0.8495 - val_accuracy: 0.7011 Epoch 5/10 938/938 [==============================] - 3s 3ms/step - loss: 0.8855 - accuracy: 0.6722 - val_loss: 0.8361 - val_accuracy: 0.6685 Epoch 6/10 938/938 [==============================] - 3s 3ms/step - loss: 0.8482 - accuracy: 0.6852 - val_loss: 0.7975 - val_accuracy: 0.6830 Epoch 7/10 938/938 [==============================] - 3s 3ms/step - loss: 0.8219 - accuracy: 0.6941 - val_loss: 0.7630 - val_accuracy: 0.6990 Epoch 8/10 938/938 [==============================] - 3s 3ms/step - loss: 0.7995 - accuracy: 0.7011 - val_loss: 0.7280 - val_accuracy: 0.7263 Epoch 9/10 938/938 [==============================] - 3s 3ms/step - loss: 0.7830 - accuracy: 0.7059 - val_loss: 0.7156 - val_accuracy: 0.7445 Epoch 10/10 938/938 [==============================] - 3s 3ms/step - loss: 0.7636 - accuracy: 0.7136 - val_loss: 0.7026 - val_accuracy: 0.7462
Definir horario CLR
El tfa.optimizers.CyclicalLearningRate módulo de retorno una programación directa que se puede pasar a un optimizador. El cronograma toma un paso como entrada y genera un valor calculado usando la fórmula CLR como se establece en el documento.
steps_per_epoch = len(x_train) // BATCH_SIZE
clr = tfa.optimizers.CyclicalLearningRate(initial_learning_rate=INIT_LR,
maximal_learning_rate=MAX_LR,
scale_fn=lambda x: 1/(2.**(x-1)),
step_size=2 * steps_per_epoch
)
optimizer = tf.keras.optimizers.SGD(clr)
A continuación, se especifican los límites inferior y superior de la tasa de aprendizaje y el horario oscilará entre ese rango ([1e-4, 1e-2] en este caso). scale_fn se utiliza para definir la función que ampliar y reducir la amplitud del ritmo de aprendizaje dentro de un ciclo determinado. step_size define la duración de un ciclo único. Un step_size de 2 significa que necesita un total de 4 iteraciones para completar un ciclo. El valor recomendado para step_size es el siguiente:
factor * steps_per_epoch donde el factor está dentro del intervalo [2, 8].
En el mismo documento de CLR , Leslie también presentó un método simple y elegante para elegir los límites de velocidad de aprendizaje. Se le anima a que lo compruebe también. Este blog ofrece una buena introducción al método.
A continuación, a visualizar cómo los clr miradas horario gusta.
step = np.arange(0, EPOCHS * steps_per_epoch)
lr = clr(step)
plt.plot(step, lr)
plt.xlabel("Steps")
plt.ylabel("Learning Rate")
plt.show()
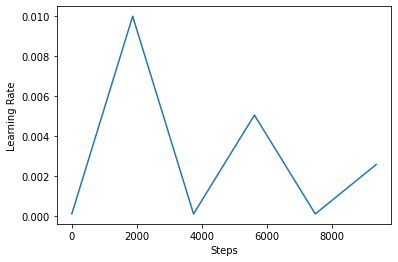
Para visualizar mejor el efecto de CLR, puede trazar el programa con un mayor número de pasos.
step = np.arange(0, 100 * steps_per_epoch)
lr = clr(step)
plt.plot(step, lr)
plt.xlabel("Steps")
plt.ylabel("Learning Rate")
plt.show()
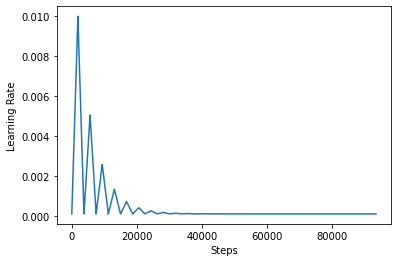
La función que está usando en este tutorial se conoce como la triangular2 método en el documento CLR. Hay otras dos funciones no se exploraron a saber triangular y exp (abreviatura de exponencial).
Entrena un modelo con CLR
clr_model = tf.keras.models.load_model("initial_model")
clr_history = train_model(clr_model, optimizer=optimizer)
WARNING:tensorflow:No training configuration found in save file, so the model was *not* compiled. Compile it manually. Epoch 1/10 938/938 [==============================] - 4s 4ms/step - loss: 2.3005 - accuracy: 0.1165 - val_loss: 2.2852 - val_accuracy: 0.2378 Epoch 2/10 938/938 [==============================] - 3s 4ms/step - loss: 2.1931 - accuracy: 0.2398 - val_loss: 1.7386 - val_accuracy: 0.4530 Epoch 3/10 938/938 [==============================] - 3s 4ms/step - loss: 1.3132 - accuracy: 0.5052 - val_loss: 1.0110 - val_accuracy: 0.6482 Epoch 4/10 938/938 [==============================] - 3s 4ms/step - loss: 1.0746 - accuracy: 0.5933 - val_loss: 0.9492 - val_accuracy: 0.6622 Epoch 5/10 938/938 [==============================] - 3s 4ms/step - loss: 1.0528 - accuracy: 0.6028 - val_loss: 0.9439 - val_accuracy: 0.6519 Epoch 6/10 938/938 [==============================] - 3s 4ms/step - loss: 1.0198 - accuracy: 0.6172 - val_loss: 0.9096 - val_accuracy: 0.6620 Epoch 7/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9778 - accuracy: 0.6339 - val_loss: 0.8784 - val_accuracy: 0.6746 Epoch 8/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9535 - accuracy: 0.6487 - val_loss: 0.8665 - val_accuracy: 0.6903 Epoch 9/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9510 - accuracy: 0.6497 - val_loss: 0.8691 - val_accuracy: 0.6857 Epoch 10/10 938/938 [==============================] - 3s 4ms/step - loss: 0.9424 - accuracy: 0.6529 - val_loss: 0.8571 - val_accuracy: 0.6917
Como se esperaba, la pérdida comienza más alta de lo habitual y luego se estabiliza a medida que avanzan los ciclos. Puede confirmar esto visualmente con los gráficos a continuación.
Visualiza pérdidas
(fig, ax) = plt.subplots(2, 1, figsize=(10, 8))
ax[0].plot(no_clr_history.history["loss"], label="train_loss")
ax[0].plot(no_clr_history.history["val_loss"], label="val_loss")
ax[0].set_title("No CLR")
ax[0].set_xlabel("Epochs")
ax[0].set_ylabel("Loss")
ax[0].set_ylim([0, 2.5])
ax[0].legend()
ax[1].plot(clr_history.history["loss"], label="train_loss")
ax[1].plot(clr_history.history["val_loss"], label="val_loss")
ax[1].set_title("CLR")
ax[1].set_xlabel("Epochs")
ax[1].set_ylabel("Loss")
ax[1].set_ylim([0, 2.5])
ax[1].legend()
fig.tight_layout(pad=3.0)
fig.show()
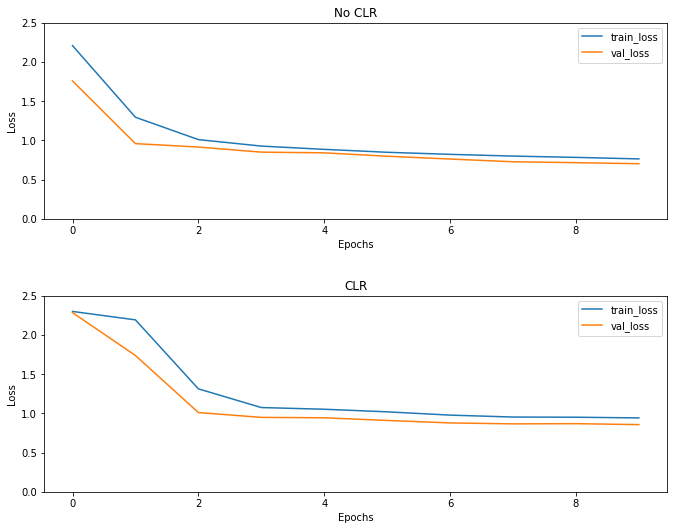
A pesar de que para este ejemplo de juguete, que no viste los efectos de CLR mucho, pero tener en cuenta que es uno de los principales ingredientes detrás de Super Convergencia y puede tener un muy buen impacto en el entrenamiento en entornos de gran escala.

