TensorFlow.org에서 보기 TensorFlow.org에서 보기 |
 Google Colab에서 실행하기 Google Colab에서 실행하기 |
 GitHub에서 소스 보기 GitHub에서 소스 보기 |
 노트북 다운로드하기 노트북 다운로드하기 |
개요
이 노트북은 애드온 패키지에서 Conditional Graident 옵티마이저를 사용하는 방법을 보여줍니다.
ConditionalGradient
신경망의 매개변수를 제한하면 기본적인 정규화 효과로 인해 훈련에 유익한 것으로 나타났습니다. 종종 매개변수는 소프트 페널티(제약 조건 만족을 보장하지 않음) 또는 프로젝션 연산(계산적으로 비쌈)을 통해 제한됩니다. 반면에 CG(Conditional Gradient) 옵티마이저는 값 비싼 프로젝션 단계 없이 제약 조건을 엄격하게 적용합니다. 제약 조건 세트 내에서 목표의 선형 근사치를 최소화하여 동작합니다. 이 노트북의 MNIST 데이터세트에서 CG 옵티마이저를 통해 Frobenius norm 제약 조건의 적용을 보여줍니다. CG는 이제 tensorflow API로 사용 가능합니다. 옵티마이저에 대한 자세한 내용은 https://arxiv.org/pdf/1803.06453.pdf를 참조하세요.
설정
pip install -q -U tensorflow-addonsimport tensorflow as tf
import tensorflow_addons as tfa
from matplotlib import pyplot as plt
# Hyperparameters
batch_size=64
epochs=10
모델 빌드하기
model_1 = tf.keras.Sequential([
tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])
데이터 준비하기
# Load MNIST dataset as NumPy arrays
dataset = {}
num_validation = 10000
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
# Preprocess the data
x_train = x_train.reshape(-1, 784).astype('float32') / 255
x_test = x_test.reshape(-1, 784).astype('float32') / 255
사용자 정의 콜백 함수 정의하기
def frobenius_norm(m):
"""This function is to calculate the frobenius norm of the matrix of all
layer's weight.
Args:
m: is a list of weights param for each layers.
"""
total_reduce_sum = 0
for i in range(len(m)):
total_reduce_sum = total_reduce_sum + tf.math.reduce_sum(m[i]**2)
norm = total_reduce_sum**0.5
return norm
CG_frobenius_norm_of_weight = []
CG_get_weight_norm = tf.keras.callbacks.LambdaCallback(
on_epoch_end=lambda batch, logs: CG_frobenius_norm_of_weight.append(
frobenius_norm(model_1.trainable_weights).numpy()))
훈련 및 평가: CG를 옵티마이저로 사용하기
일반적인 keras 옵티마이저를 새로운 tfa 옵티마이저로 간단히 교체합니다.
# Compile the model
model_1.compile(
optimizer=tfa.optimizers.ConditionalGradient(
learning_rate=0.99949, lambda_=203), # Utilize TFA optimizer
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=['accuracy'])
history_cg = model_1.fit(
x_train,
y_train,
batch_size=batch_size,
validation_data=(x_test, y_test),
epochs=epochs,
callbacks=[CG_get_weight_norm])
Epoch 1/10 938/938 [==============================] - 3s 3ms/step - loss: 0.3775 - accuracy: 0.8859 - val_loss: 0.2121 - val_accuracy: 0.9358 Epoch 2/10 938/938 [==============================] - 2s 3ms/step - loss: 0.1916 - accuracy: 0.9423 - val_loss: 0.1583 - val_accuracy: 0.9516 Epoch 3/10 938/938 [==============================] - 2s 3ms/step - loss: 0.1533 - accuracy: 0.9540 - val_loss: 0.1763 - val_accuracy: 0.9428 Epoch 4/10 938/938 [==============================] - 2s 3ms/step - loss: 0.1347 - accuracy: 0.9595 - val_loss: 0.1292 - val_accuracy: 0.9601 Epoch 5/10 938/938 [==============================] - 2s 3ms/step - loss: 0.1226 - accuracy: 0.9627 - val_loss: 0.1129 - val_accuracy: 0.9661 Epoch 6/10 938/938 [==============================] - 2s 3ms/step - loss: 0.1164 - accuracy: 0.9639 - val_loss: 0.1418 - val_accuracy: 0.9586 Epoch 7/10 938/938 [==============================] - 2s 3ms/step - loss: 0.1112 - accuracy: 0.9659 - val_loss: 0.1108 - val_accuracy: 0.9643 Epoch 8/10 938/938 [==============================] - 2s 3ms/step - loss: 0.1089 - accuracy: 0.9666 - val_loss: 0.1114 - val_accuracy: 0.9675 Epoch 9/10 938/938 [==============================] - 2s 3ms/step - loss: 0.1057 - accuracy: 0.9677 - val_loss: 0.1072 - val_accuracy: 0.9654 Epoch 10/10 938/938 [==============================] - 2s 3ms/step - loss: 0.1039 - accuracy: 0.9683 - val_loss: 0.1197 - val_accuracy: 0.9627
훈련 및 평가: SGD를 옵티마이저로 사용하기
model_2 = tf.keras.Sequential([
tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])
SGD_frobenius_norm_of_weight = []
SGD_get_weight_norm = tf.keras.callbacks.LambdaCallback(
on_epoch_end=lambda batch, logs: SGD_frobenius_norm_of_weight.append(
frobenius_norm(model_2.trainable_weights).numpy()))
# Compile the model
model_2.compile(
optimizer=tf.keras.optimizers.SGD(0.01), # Utilize SGD optimizer
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=['accuracy'])
history_sgd = model_2.fit(
x_train,
y_train,
batch_size=batch_size,
validation_data=(x_test, y_test),
epochs=epochs,
callbacks=[SGD_get_weight_norm])
Epoch 1/10 938/938 [==============================] - 2s 2ms/step - loss: 1.0198 - accuracy: 0.7126 - val_loss: 0.4461 - val_accuracy: 0.8761 Epoch 2/10 938/938 [==============================] - 2s 2ms/step - loss: 0.3951 - accuracy: 0.8888 - val_loss: 0.3319 - val_accuracy: 0.9061 Epoch 3/10 938/938 [==============================] - 2s 2ms/step - loss: 0.3221 - accuracy: 0.9070 - val_loss: 0.2851 - val_accuracy: 0.9182 Epoch 4/10 938/938 [==============================] - 2s 2ms/step - loss: 0.2855 - accuracy: 0.9170 - val_loss: 0.2595 - val_accuracy: 0.9255 Epoch 5/10 938/938 [==============================] - 2s 2ms/step - loss: 0.2603 - accuracy: 0.9239 - val_loss: 0.2371 - val_accuracy: 0.9304 Epoch 6/10 938/938 [==============================] - 2s 2ms/step - loss: 0.2408 - accuracy: 0.9301 - val_loss: 0.2235 - val_accuracy: 0.9335 Epoch 7/10 938/938 [==============================] - 2s 2ms/step - loss: 0.2243 - accuracy: 0.9349 - val_loss: 0.2084 - val_accuracy: 0.9390 Epoch 8/10 938/938 [==============================] - 2s 2ms/step - loss: 0.2107 - accuracy: 0.9384 - val_loss: 0.1987 - val_accuracy: 0.9413 Epoch 9/10 938/938 [==============================] - 2s 2ms/step - loss: 0.1986 - accuracy: 0.9426 - val_loss: 0.1870 - val_accuracy: 0.9453 Epoch 10/10 938/938 [==============================] - 2s 2ms/step - loss: 0.1877 - accuracy: 0.9457 - val_loss: 0.1786 - val_accuracy: 0.9473
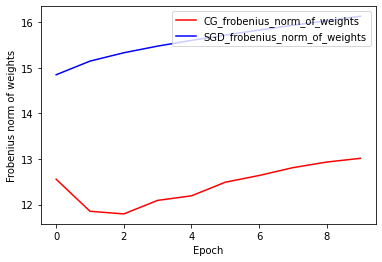
가중치의 Frobenius Norm: CG vs SGD
CG 옵티마이저의 현재 구현은 Frobenius Norm을 기반으로 하며 Frobenius Norm을 대상 함수의 regularizer로 간주합니다. 따라서 CG의 정규화 효과를 Frobenius Norm regularizer를 부과하지 않은 SGD 옵티마이저와 비교합니다.
plt.plot(
CG_frobenius_norm_of_weight,
color='r',
label='CG_frobenius_norm_of_weights')
plt.plot(
SGD_frobenius_norm_of_weight,
color='b',
label='SGD_frobenius_norm_of_weights')
plt.xlabel('Epoch')
plt.ylabel('Frobenius norm of weights')
plt.legend(loc=1)
<matplotlib.legend.Legend at 0x7fdf68259cc0>
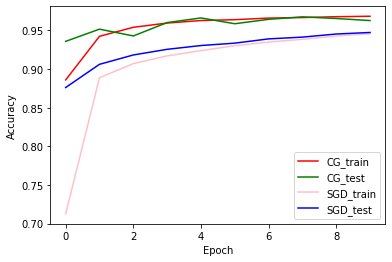
훈련 및 검증 정확성: CG vs SGD
plt.plot(history_cg.history['accuracy'], color='r', label='CG_train')
plt.plot(history_cg.history['val_accuracy'], color='g', label='CG_test')
plt.plot(history_sgd.history['accuracy'], color='pink', label='SGD_train')
plt.plot(history_sgd.history['val_accuracy'], color='b', label='SGD_test')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend(loc=4)
<matplotlib.legend.Legend at 0x7fdf68582f98>