Ottimizzatori di componenti aggiuntivi TensorFlow: ConditionalGradient,Ottimizzatori di componenti aggiuntivi TensorFlow: ConditionalGradient

Visualizza su TensorFlow.org Esegui in Google Colab Visualizza la fonte su GitHub Scarica taccuino

Panoramica

Questo notebook dimostrerà come utilizzare Conditional Graident Optimizer dal pacchetto Addons.

Gradiente condizionale

È stato dimostrato che limitare i parametri di una rete neurale è utile nell'allenamento a causa degli effetti di regolarizzazione sottostanti. Spesso, i parametri sono vincolati tramite una penalità morbida (che non garantisce mai la soddisfazione del vincolo) o tramite un'operazione di proiezione (che è computazionalmente costosa). L'ottimizzatore del gradiente condizionale (CG), d'altra parte, applica i vincoli rigorosamente senza la necessità di un costoso passaggio di proiezione. Funziona minimizzando un'approssimazione lineare dell'obiettivo all'interno dell'insieme di vincoli. In questo taccuino, dimostrerai l'applicazione del vincolo della norma di Frobenius tramite l'ottimizzatore CG sul set di dati MNIST. CG è ora disponibile come API tensorflow. Per maggiori dettagli sul ottimizzatore sono disponibili presso https://arxiv.org/pdf/1803.06453.pdf

Impostare

pip install -q -U tensorflow-addons

import tensorflow as tf
import tensorflow_addons as tfa
from matplotlib import pyplot as plt

# Hyperparameters
batch_size=64
epochs=10

Costruisci il modello

model_1 = tf.keras.Sequential([
    tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
    tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
    tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])

Prepara i dati

# Load MNIST dataset as NumPy arrays
dataset = {}
num_validation = 10000
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()

# Preprocess the data
x_train = x_train.reshape(-1, 784).astype('float32') / 255
x_test = x_test.reshape(-1, 784).astype('float32') / 255

Definire una funzione di richiamata personalizzata

def frobenius_norm(m):
    """This function is to calculate the frobenius norm of the matrix of all
    layer's weight.

    Args:
        m: is a list of weights param for each layers.
    """
    total_reduce_sum = 0
    for i in range(len(m)):
        total_reduce_sum = total_reduce_sum + tf.math.reduce_sum(m[i]**2)
    norm = total_reduce_sum**0.5
    return norm

CG_frobenius_norm_of_weight = []
CG_get_weight_norm = tf.keras.callbacks.LambdaCallback(
    on_epoch_end=lambda batch, logs: CG_frobenius_norm_of_weight.append(
        frobenius_norm(model_1.trainable_weights).numpy()))

Addestra e valuta: utilizzo della computer grafica come ottimizzatore

Sostituisci semplicemente i tipici ottimizzatori keras con il nuovo ottimizzatore tfa

# Compile the model
model_1.compile(
    optimizer=tfa.optimizers.ConditionalGradient(
        learning_rate=0.99949, lambda_=203),  # Utilize TFA optimizer
    loss=tf.keras.losses.SparseCategoricalCrossentropy(),
    metrics=['accuracy'])

history_cg = model_1.fit(
    x_train,
    y_train,
    batch_size=batch_size,
    validation_data=(x_test, y_test),
    epochs=epochs,
    callbacks=[CG_get_weight_norm])

Epoch 1/10
938/938 [==============================] - 4s 3ms/step - loss: 0.6034 - accuracy: 0.8162 - val_loss: 0.2282 - val_accuracy: 0.9313
Epoch 2/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1968 - accuracy: 0.9411 - val_loss: 0.1865 - val_accuracy: 0.9411
Epoch 3/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1502 - accuracy: 0.9552 - val_loss: 0.1356 - val_accuracy: 0.9590
Epoch 4/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1349 - accuracy: 0.9598 - val_loss: 0.1084 - val_accuracy: 0.9679
Epoch 5/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1261 - accuracy: 0.9609 - val_loss: 0.1162 - val_accuracy: 0.9648
Epoch 6/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1119 - accuracy: 0.9662 - val_loss: 0.1277 - val_accuracy: 0.9567
Epoch 7/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1096 - accuracy: 0.9671 - val_loss: 0.1009 - val_accuracy: 0.9685
Epoch 8/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1045 - accuracy: 0.9687 - val_loss: 0.1015 - val_accuracy: 0.9698
Epoch 9/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1011 - accuracy: 0.9688 - val_loss: 0.1180 - val_accuracy: 0.9627
Epoch 10/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1029 - accuracy: 0.9689 - val_loss: 0.1590 - val_accuracy: 0.9516

Formazione e valutazione: utilizzo di SGD come ottimizzatore

model_2 = tf.keras.Sequential([
    tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
    tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
    tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])

SGD_frobenius_norm_of_weight = []
SGD_get_weight_norm = tf.keras.callbacks.LambdaCallback(
    on_epoch_end=lambda batch, logs: SGD_frobenius_norm_of_weight.append(
        frobenius_norm(model_2.trainable_weights).numpy()))

# Compile the model
model_2.compile(
    optimizer=tf.keras.optimizers.SGD(0.01),  # Utilize SGD optimizer
    loss=tf.keras.losses.SparseCategoricalCrossentropy(),
    metrics=['accuracy'])

history_sgd = model_2.fit(
    x_train,
    y_train,
    batch_size=batch_size,
    validation_data=(x_test, y_test),
    epochs=epochs,
    callbacks=[SGD_get_weight_norm])

Epoch 1/10
938/938 [==============================] - 3s 3ms/step - loss: 1.4885 - accuracy: 0.5945 - val_loss: 0.4230 - val_accuracy: 0.8838
Epoch 2/10
938/938 [==============================] - 2s 2ms/step - loss: 0.4087 - accuracy: 0.8875 - val_loss: 0.3222 - val_accuracy: 0.9073
Epoch 3/10
938/938 [==============================] - 2s 2ms/step - loss: 0.3267 - accuracy: 0.9075 - val_loss: 0.2867 - val_accuracy: 0.9178
Epoch 4/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2903 - accuracy: 0.9186 - val_loss: 0.2605 - val_accuracy: 0.9259
Epoch 5/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2691 - accuracy: 0.9233 - val_loss: 0.2468 - val_accuracy: 0.9292
Epoch 6/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2466 - accuracy: 0.9291 - val_loss: 0.2265 - val_accuracy: 0.9352
Epoch 7/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2210 - accuracy: 0.9370 - val_loss: 0.2106 - val_accuracy: 0.9404
Epoch 8/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2137 - accuracy: 0.9387 - val_loss: 0.2029 - val_accuracy: 0.9424
Epoch 9/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1996 - accuracy: 0.9429 - val_loss: 0.1937 - val_accuracy: 0.9441
Epoch 10/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1925 - accuracy: 0.9450 - val_loss: 0.1831 - val_accuracy: 0.9469

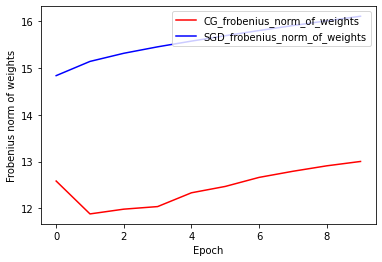
Norma dei pesi di Frobenius: CG vs SGD

L'attuale implementazione dell'ottimizzatore CG si basa su Frobenius Norm, considerando Frobenius Norm come regolarizzatore nella funzione di destinazione. Pertanto, si confronta l'effetto regolarizzato di CG con l'ottimizzatore SGD, che non ha imposto il regolarizzatore Frobenius Norm.

plt.plot(
    CG_frobenius_norm_of_weight,
    color='r',
    label='CG_frobenius_norm_of_weights')
plt.plot(
    SGD_frobenius_norm_of_weight,
    color='b',
    label='SGD_frobenius_norm_of_weights')
plt.xlabel('Epoch')
plt.ylabel('Frobenius norm of weights')
plt.legend(loc=1)

<matplotlib.legend.Legend at 0x7fada7ab12e8>

png

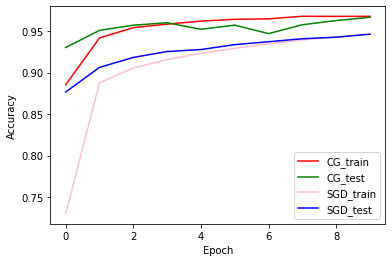
Precisione di addestramento e convalida: CG vs SGD

plt.plot(history_cg.history['accuracy'], color='r', label='CG_train')
plt.plot(history_cg.history['val_accuracy'], color='g', label='CG_test')
plt.plot(history_sgd.history['accuracy'], color='pink', label='SGD_train')
plt.plot(history_sgd.history['val_accuracy'], color='b', label='SGD_test')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend(loc=4)

<matplotlib.legend.Legend at 0x7fada7983e80>

png