הצג באתר TensorFlow.org

הפעל בגוגל קולאב

צפה במקור ב-GitHub

הורד מחברת

סקירה כללית

מחברת זו תדגים כיצד להשתמש ב-Conditional Graident Optimizer מחבילת Addons.

ConditionalGradient

הגבלת הפרמטרים של רשת עצבית הוכחה כמועילה באימון בגלל השפעות ההסדרה הבסיסיות. לעתים קרובות, פרמטרים מוגבלים באמצעות עונש רך (שאף פעם לא מבטיח את שביעות הרצון של האילוץ) או באמצעות פעולת הקרנה (שהיא יקרה מבחינה חישובית). אופטימיזציית דרגות מותנית (CG), לעומת זאת, אוכפת את האילוצים אך ורק ללא צורך בצעד הקרנה יקר. זה עובד על ידי מזעור קירוב ליניארי של המטרה בתוך קבוצת האילוצים. במחברת זו, אתה מדגים את היישום של אילוץ הנורמה של Frobenius באמצעות כלי האופטימיזציה של CG במערך הנתונים של MNIST. CG זמין כעת כ- API של tensorflow. עוד פרטים על האופטימיזציה זמינים https://arxiv.org/pdf/1803.06453.pdf

להכין

pip install -q -U tensorflow-addons

import tensorflow as tf
import tensorflow_addons as tfa
from matplotlib import pyplot as plt

# Hyperparameters
batch_size=64
epochs=10

בנה את המודל

model_1 = tf.keras.Sequential([
    tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
    tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
    tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])

הכן את הנתונים

# Load MNIST dataset as NumPy arrays
dataset = {}
num_validation = 10000
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()

# Preprocess the data
x_train = x_train.reshape(-1, 784).astype('float32') / 255
x_test = x_test.reshape(-1, 784).astype('float32') / 255

הגדר פונקציית התקשרות חוזרת מותאמת אישית

def frobenius_norm(m):
    """This function is to calculate the frobenius norm of the matrix of all
    layer's weight.

    Args:
        m: is a list of weights param for each layers.
    """
    total_reduce_sum = 0
    for i in range(len(m)):
        total_reduce_sum = total_reduce_sum + tf.math.reduce_sum(m[i]**2)
    norm = total_reduce_sum**0.5
    return norm

CG_frobenius_norm_of_weight = []
CG_get_weight_norm = tf.keras.callbacks.LambdaCallback(
    on_epoch_end=lambda batch, logs: CG_frobenius_norm_of_weight.append(
        frobenius_norm(model_1.trainable_weights).numpy()))

אימון והערכת: שימוש ב-CG כמייעל

כל שעליך לעשות הוא להחליף את אופטימיזציית keras טיפוסית במייעל tfa החדש

# Compile the model
model_1.compile(
    optimizer=tfa.optimizers.ConditionalGradient(
        learning_rate=0.99949, lambda_=203),  # Utilize TFA optimizer
    loss=tf.keras.losses.SparseCategoricalCrossentropy(),
    metrics=['accuracy'])

history_cg = model_1.fit(
    x_train,
    y_train,
    batch_size=batch_size,
    validation_data=(x_test, y_test),
    epochs=epochs,
    callbacks=[CG_get_weight_norm])

Epoch 1/10
938/938 [==============================] - 4s 3ms/step - loss: 0.6034 - accuracy: 0.8162 - val_loss: 0.2282 - val_accuracy: 0.9313
Epoch 2/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1968 - accuracy: 0.9411 - val_loss: 0.1865 - val_accuracy: 0.9411
Epoch 3/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1502 - accuracy: 0.9552 - val_loss: 0.1356 - val_accuracy: 0.9590
Epoch 4/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1349 - accuracy: 0.9598 - val_loss: 0.1084 - val_accuracy: 0.9679
Epoch 5/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1261 - accuracy: 0.9609 - val_loss: 0.1162 - val_accuracy: 0.9648
Epoch 6/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1119 - accuracy: 0.9662 - val_loss: 0.1277 - val_accuracy: 0.9567
Epoch 7/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1096 - accuracy: 0.9671 - val_loss: 0.1009 - val_accuracy: 0.9685
Epoch 8/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1045 - accuracy: 0.9687 - val_loss: 0.1015 - val_accuracy: 0.9698
Epoch 9/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1011 - accuracy: 0.9688 - val_loss: 0.1180 - val_accuracy: 0.9627
Epoch 10/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1029 - accuracy: 0.9689 - val_loss: 0.1590 - val_accuracy: 0.9516

אימון והערכת: שימוש ב-SGD כמייעל

model_2 = tf.keras.Sequential([
    tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
    tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
    tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])

SGD_frobenius_norm_of_weight = []
SGD_get_weight_norm = tf.keras.callbacks.LambdaCallback(
    on_epoch_end=lambda batch, logs: SGD_frobenius_norm_of_weight.append(
        frobenius_norm(model_2.trainable_weights).numpy()))

# Compile the model
model_2.compile(
    optimizer=tf.keras.optimizers.SGD(0.01),  # Utilize SGD optimizer
    loss=tf.keras.losses.SparseCategoricalCrossentropy(),
    metrics=['accuracy'])

history_sgd = model_2.fit(
    x_train,
    y_train,
    batch_size=batch_size,
    validation_data=(x_test, y_test),
    epochs=epochs,
    callbacks=[SGD_get_weight_norm])

Epoch 1/10
938/938 [==============================] - 3s 3ms/step - loss: 1.4885 - accuracy: 0.5945 - val_loss: 0.4230 - val_accuracy: 0.8838
Epoch 2/10
938/938 [==============================] - 2s 2ms/step - loss: 0.4087 - accuracy: 0.8875 - val_loss: 0.3222 - val_accuracy: 0.9073
Epoch 3/10
938/938 [==============================] - 2s 2ms/step - loss: 0.3267 - accuracy: 0.9075 - val_loss: 0.2867 - val_accuracy: 0.9178
Epoch 4/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2903 - accuracy: 0.9186 - val_loss: 0.2605 - val_accuracy: 0.9259
Epoch 5/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2691 - accuracy: 0.9233 - val_loss: 0.2468 - val_accuracy: 0.9292
Epoch 6/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2466 - accuracy: 0.9291 - val_loss: 0.2265 - val_accuracy: 0.9352
Epoch 7/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2210 - accuracy: 0.9370 - val_loss: 0.2106 - val_accuracy: 0.9404
Epoch 8/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2137 - accuracy: 0.9387 - val_loss: 0.2029 - val_accuracy: 0.9424
Epoch 9/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1996 - accuracy: 0.9429 - val_loss: 0.1937 - val_accuracy: 0.9441
Epoch 10/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1925 - accuracy: 0.9450 - val_loss: 0.1831 - val_accuracy: 0.9469

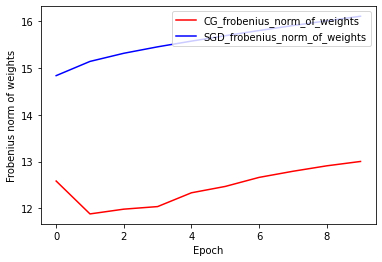
נורמת המשקולות של Frobenius: CG לעומת SGD

היישום הנוכחי של CG Optimizer מבוסס על Frobenius Norm, תוך התייחסות Frobenius Norm כמסדרת בפונקציית היעד. לכן, אתה משווה את האפקט המוסדר של CG עם אופטימיזציית SGD, שלא כפה מסדרת Frobenius Norm.

plt.plot(
    CG_frobenius_norm_of_weight,
    color='r',
    label='CG_frobenius_norm_of_weights')
plt.plot(
    SGD_frobenius_norm_of_weight,
    color='b',
    label='SGD_frobenius_norm_of_weights')
plt.xlabel('Epoch')
plt.ylabel('Frobenius norm of weights')
plt.legend(loc=1)

<matplotlib.legend.Legend at 0x7fada7ab12e8>

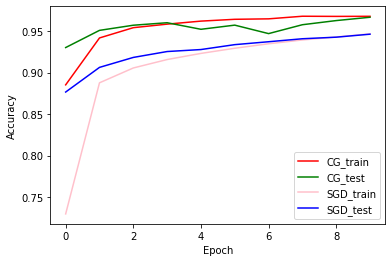
דיוק הרכבות ואימות: CG לעומת SGD

plt.plot(history_cg.history['accuracy'], color='r', label='CG_train')
plt.plot(history_cg.history['val_accuracy'], color='g', label='CG_test')
plt.plot(history_sgd.history['accuracy'], color='pink', label='SGD_train')
plt.plot(history_sgd.history['val_accuracy'], color='b', label='SGD_test')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend(loc=4)

<matplotlib.legend.Legend at 0x7fada7983e80>