TensorFlow.org এ দেখুন

Google Colab-এ চালান

GitHub-এ উৎস দেখুন

নোটবুক ডাউনলোড করুন

ওভারভিউ

এই নোটবুকটি প্রদর্শন করবে কিভাবে অ্যাডঅন প্যাকেজ থেকে কন্ডিশনাল গ্রেডেন্ট অপ্টিমাইজার ব্যবহার করতে হয়।

শর্তসাপেক্ষ গ্রেডিয়েন্ট

অন্তর্নিহিত নিয়মিতকরণের প্রভাবের কারণে একটি নিউরাল নেটওয়ার্কের পরামিতিগুলিকে সীমাবদ্ধ করা প্রশিক্ষণে উপকারী বলে দেখানো হয়েছে। প্রায়শই, প্যারামিটারগুলি একটি নরম জরিমানা (যা কখনই সীমাবদ্ধতার সন্তুষ্টির গ্যারান্টি দেয় না) বা একটি প্রজেকশন অপারেশন (যা গণনাগতভাবে ব্যয়বহুল) মাধ্যমে সীমাবদ্ধ থাকে। অন্যদিকে কন্ডিশনাল গ্রেডিয়েন্ট (CG) অপ্টিমাইজার, একটি ব্যয়বহুল প্রজেকশন পদক্ষেপের প্রয়োজন ছাড়াই কঠোরভাবে সীমাবদ্ধতা প্রয়োগ করে। এটি সীমাবদ্ধতার সেটের মধ্যে উদ্দেশ্যটির একটি রৈখিক অনুমান কমিয়ে কাজ করে। এই নোটবুকে, আপনি MNIST ডেটাসেটে CG অপ্টিমাইজারের মাধ্যমে Frobenius আদর্শ সীমাবদ্ধতার প্রয়োগ প্রদর্শন করেন। CG এখন একটি tensorflow API হিসাবে উপলব্ধ। অপটিমাইজার এর আরো বিস্তারিত পাওয়া যায় https://arxiv.org/pdf/1803.06453.pdf

সেটআপ

pip install -q -U tensorflow-addons

import tensorflow as tf
import tensorflow_addons as tfa
from matplotlib import pyplot as plt

# Hyperparameters
batch_size=64
epochs=10

মডেল তৈরি করুন

model_1 = tf.keras.Sequential([
    tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
    tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
    tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])

ডেটা প্রস্তুত করুন

# Load MNIST dataset as NumPy arrays
dataset = {}
num_validation = 10000
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()

# Preprocess the data
x_train = x_train.reshape(-1, 784).astype('float32') / 255
x_test = x_test.reshape(-1, 784).astype('float32') / 255

একটি কাস্টম কলব্যাক ফাংশন সংজ্ঞায়িত করুন

def frobenius_norm(m):
    """This function is to calculate the frobenius norm of the matrix of all
    layer's weight.

    Args:
        m: is a list of weights param for each layers.
    """
    total_reduce_sum = 0
    for i in range(len(m)):
        total_reduce_sum = total_reduce_sum + tf.math.reduce_sum(m[i]**2)
    norm = total_reduce_sum**0.5
    return norm

CG_frobenius_norm_of_weight = []
CG_get_weight_norm = tf.keras.callbacks.LambdaCallback(
    on_epoch_end=lambda batch, logs: CG_frobenius_norm_of_weight.append(
        frobenius_norm(model_1.trainable_weights).numpy()))

ট্রেন এবং মূল্যায়ন: অপ্টিমাইজার হিসাবে সিজি ব্যবহার করা

সাধারণ কেরাস অপ্টিমাইজারগুলিকে নতুন টিএফএ অপ্টিমাইজারের সাথে প্রতিস্থাপন করুন৷

# Compile the model
model_1.compile(
    optimizer=tfa.optimizers.ConditionalGradient(
        learning_rate=0.99949, lambda_=203),  # Utilize TFA optimizer
    loss=tf.keras.losses.SparseCategoricalCrossentropy(),
    metrics=['accuracy'])

history_cg = model_1.fit(
    x_train,
    y_train,
    batch_size=batch_size,
    validation_data=(x_test, y_test),
    epochs=epochs,
    callbacks=[CG_get_weight_norm])

Epoch 1/10
938/938 [==============================] - 4s 3ms/step - loss: 0.6034 - accuracy: 0.8162 - val_loss: 0.2282 - val_accuracy: 0.9313
Epoch 2/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1968 - accuracy: 0.9411 - val_loss: 0.1865 - val_accuracy: 0.9411
Epoch 3/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1502 - accuracy: 0.9552 - val_loss: 0.1356 - val_accuracy: 0.9590
Epoch 4/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1349 - accuracy: 0.9598 - val_loss: 0.1084 - val_accuracy: 0.9679
Epoch 5/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1261 - accuracy: 0.9609 - val_loss: 0.1162 - val_accuracy: 0.9648
Epoch 6/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1119 - accuracy: 0.9662 - val_loss: 0.1277 - val_accuracy: 0.9567
Epoch 7/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1096 - accuracy: 0.9671 - val_loss: 0.1009 - val_accuracy: 0.9685
Epoch 8/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1045 - accuracy: 0.9687 - val_loss: 0.1015 - val_accuracy: 0.9698
Epoch 9/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1011 - accuracy: 0.9688 - val_loss: 0.1180 - val_accuracy: 0.9627
Epoch 10/10
938/938 [==============================] - 3s 3ms/step - loss: 0.1029 - accuracy: 0.9689 - val_loss: 0.1590 - val_accuracy: 0.9516

ট্রেন এবং মূল্যায়ন: অপ্টিমাইজার হিসাবে SGD ব্যবহার করা

model_2 = tf.keras.Sequential([
    tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
    tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
    tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])

SGD_frobenius_norm_of_weight = []
SGD_get_weight_norm = tf.keras.callbacks.LambdaCallback(
    on_epoch_end=lambda batch, logs: SGD_frobenius_norm_of_weight.append(
        frobenius_norm(model_2.trainable_weights).numpy()))

# Compile the model
model_2.compile(
    optimizer=tf.keras.optimizers.SGD(0.01),  # Utilize SGD optimizer
    loss=tf.keras.losses.SparseCategoricalCrossentropy(),
    metrics=['accuracy'])

history_sgd = model_2.fit(
    x_train,
    y_train,
    batch_size=batch_size,
    validation_data=(x_test, y_test),
    epochs=epochs,
    callbacks=[SGD_get_weight_norm])

Epoch 1/10
938/938 [==============================] - 3s 3ms/step - loss: 1.4885 - accuracy: 0.5945 - val_loss: 0.4230 - val_accuracy: 0.8838
Epoch 2/10
938/938 [==============================] - 2s 2ms/step - loss: 0.4087 - accuracy: 0.8875 - val_loss: 0.3222 - val_accuracy: 0.9073
Epoch 3/10
938/938 [==============================] - 2s 2ms/step - loss: 0.3267 - accuracy: 0.9075 - val_loss: 0.2867 - val_accuracy: 0.9178
Epoch 4/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2903 - accuracy: 0.9186 - val_loss: 0.2605 - val_accuracy: 0.9259
Epoch 5/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2691 - accuracy: 0.9233 - val_loss: 0.2468 - val_accuracy: 0.9292
Epoch 6/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2466 - accuracy: 0.9291 - val_loss: 0.2265 - val_accuracy: 0.9352
Epoch 7/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2210 - accuracy: 0.9370 - val_loss: 0.2106 - val_accuracy: 0.9404
Epoch 8/10
938/938 [==============================] - 2s 2ms/step - loss: 0.2137 - accuracy: 0.9387 - val_loss: 0.2029 - val_accuracy: 0.9424
Epoch 9/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1996 - accuracy: 0.9429 - val_loss: 0.1937 - val_accuracy: 0.9441
Epoch 10/10
938/938 [==============================] - 2s 2ms/step - loss: 0.1925 - accuracy: 0.9450 - val_loss: 0.1831 - val_accuracy: 0.9469

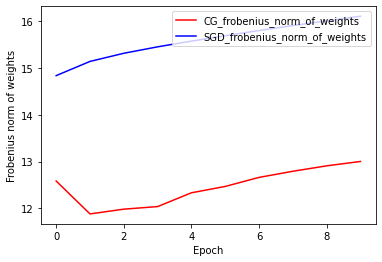
ওজনের ফ্রোবেনিয়াস আদর্শ: সিজি বনাম এসজিডি

CG অপ্টিমাইজারের বর্তমান বাস্তবায়ন Frobenius Norm-এর উপর ভিত্তি করে, Frobenius Norm-কে লক্ষ্য ফাংশনে নিয়মিত হিসাবে বিবেচনা করে। অতএব, আপনি SGD অপ্টিমাইজারের সাথে CG-এর রেগুলারাইজড ইফেক্টের তুলনা করেন, যেটি Frobenius Norm রেগুলারাইজার আরোপ করেনি।

plt.plot(
    CG_frobenius_norm_of_weight,
    color='r',
    label='CG_frobenius_norm_of_weights')
plt.plot(
    SGD_frobenius_norm_of_weight,
    color='b',
    label='SGD_frobenius_norm_of_weights')
plt.xlabel('Epoch')
plt.ylabel('Frobenius norm of weights')
plt.legend(loc=1)

<matplotlib.legend.Legend at 0x7fada7ab12e8>

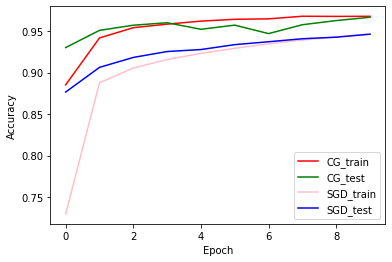
ট্রেন এবং বৈধতা নির্ভুলতা: সিজি বনাম এসজিডি

plt.plot(history_cg.history['accuracy'], color='r', label='CG_train')
plt.plot(history_cg.history['val_accuracy'], color='g', label='CG_test')
plt.plot(history_sgd.history['accuracy'], color='pink', label='SGD_train')
plt.plot(history_sgd.history['val_accuracy'], color='b', label='SGD_test')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend(loc=4)

<matplotlib.legend.Legend at 0x7fada7983e80>