Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Aperçu
Ce bloc-notes montrera comment utiliser la couche de normalisation du poids et comment elle peut améliorer la convergence.
PoidsNormalisation
Un reparamétrage simple pour accélérer la formation des réseaux de neurones profonds :
Tim Salimans, Diederik P. Kingma (2016)
En reparamétrant les poids de cette manière, vous améliorez le conditionnement du problème d'optimisation et accélérez la convergence de la descente de gradient stochastique. Notre reparamétrage s'inspire de la normalisation batch mais n'introduit aucune dépendance entre les exemples d'un minibatch. Cela signifie que notre méthode peut également être appliquée avec succès à des modèles récurrents tels que les LSTM et à des applications sensibles au bruit telles que l'apprentissage par renforcement profond ou les modèles génératifs, pour lesquels la normalisation par lots est moins bien adaptée. Bien que notre méthode soit beaucoup plus simple, elle fournit toujours une grande partie de l'accélération de la normalisation complète des lots. De plus, la surcharge de calcul de notre méthode est plus faible, ce qui permet de prendre plus d'étapes d'optimisation dans le même laps de temps.
Installer
pip install -q -U tensorflow-addons
import tensorflow as tf
import tensorflow_addons as tfa
import numpy as np
from matplotlib import pyplot as plt
# Hyper Parameters
batch_size = 32
epochs = 10
num_classes=10
Construire des modèles
# Standard ConvNet
reg_model = tf.keras.Sequential([
tf.keras.layers.Conv2D(6, 5, activation='relu'),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Conv2D(16, 5, activation='relu'),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(120, activation='relu'),
tf.keras.layers.Dense(84, activation='relu'),
tf.keras.layers.Dense(num_classes, activation='softmax'),
])
# WeightNorm ConvNet
wn_model = tf.keras.Sequential([
tfa.layers.WeightNormalization(tf.keras.layers.Conv2D(6, 5, activation='relu')),
tf.keras.layers.MaxPooling2D(2, 2),
tfa.layers.WeightNormalization(tf.keras.layers.Conv2D(16, 5, activation='relu')),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Flatten(),
tfa.layers.WeightNormalization(tf.keras.layers.Dense(120, activation='relu')),
tfa.layers.WeightNormalization(tf.keras.layers.Dense(84, activation='relu')),
tfa.layers.WeightNormalization(tf.keras.layers.Dense(num_classes, activation='softmax')),
])
Charger les données
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
# Convert class vectors to binary class matrices.
y_train = tf.keras.utils.to_categorical(y_train, num_classes)
y_test = tf.keras.utils.to_categorical(y_test, num_classes)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
Downloading data from https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz 170500096/170498071 [==============================] - 11s 0us/step
Modèles de trains
reg_model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'])
reg_history = reg_model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
Epoch 1/10 1563/1563 [==============================] - 9s 4ms/step - loss: 1.8336 - accuracy: 0.3253 - val_loss: 1.4039 - val_accuracy: 0.4957 Epoch 2/10 1563/1563 [==============================] - 5s 3ms/step - loss: 1.3773 - accuracy: 0.5039 - val_loss: 1.3419 - val_accuracy: 0.5309 Epoch 3/10 1563/1563 [==============================] - 5s 3ms/step - loss: 1.2510 - accuracy: 0.5497 - val_loss: 1.2108 - val_accuracy: 0.5710 Epoch 4/10 1563/1563 [==============================] - 5s 3ms/step - loss: 1.1606 - accuracy: 0.5858 - val_loss: 1.2134 - val_accuracy: 0.5687 Epoch 5/10 1563/1563 [==============================] - 5s 3ms/step - loss: 1.0971 - accuracy: 0.6100 - val_loss: 1.1534 - val_accuracy: 0.5880 Epoch 6/10 1563/1563 [==============================] - 5s 3ms/step - loss: 1.0420 - accuracy: 0.6296 - val_loss: 1.1944 - val_accuracy: 0.5865 Epoch 7/10 1563/1563 [==============================] - 5s 3ms/step - loss: 1.0014 - accuracy: 0.6445 - val_loss: 1.1386 - val_accuracy: 0.6012 Epoch 8/10 1563/1563 [==============================] - 5s 3ms/step - loss: 0.9550 - accuracy: 0.6623 - val_loss: 1.1659 - val_accuracy: 0.6020 Epoch 9/10 1563/1563 [==============================] - 5s 3ms/step - loss: 0.9196 - accuracy: 0.6737 - val_loss: 1.1539 - val_accuracy: 0.6027 Epoch 10/10 1563/1563 [==============================] - 5s 3ms/step - loss: 0.8768 - accuracy: 0.6889 - val_loss: 1.1509 - val_accuracy: 0.6029
wn_model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'])
wn_history = wn_model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
Epoch 1/10 1563/1563 [==============================] - 14s 8ms/step - loss: 1.8195 - accuracy: 0.3319 - val_loss: 1.4563 - val_accuracy: 0.4721 Epoch 2/10 1563/1563 [==============================] - 10s 7ms/step - loss: 1.4049 - accuracy: 0.4937 - val_loss: 1.3051 - val_accuracy: 0.5301 Epoch 3/10 1563/1563 [==============================] - 10s 6ms/step - loss: 1.2669 - accuracy: 0.5461 - val_loss: 1.2858 - val_accuracy: 0.5425 Epoch 4/10 1563/1563 [==============================] - 10s 6ms/step - loss: 1.1622 - accuracy: 0.5868 - val_loss: 1.2278 - val_accuracy: 0.5587 Epoch 5/10 1563/1563 [==============================] - 10s 6ms/step - loss: 1.0782 - accuracy: 0.6175 - val_loss: 1.1755 - val_accuracy: 0.5825 Epoch 6/10 1563/1563 [==============================] - 10s 6ms/step - loss: 1.0280 - accuracy: 0.6383 - val_loss: 1.1772 - val_accuracy: 0.5827 Epoch 7/10 1563/1563 [==============================] - 10s 6ms/step - loss: 0.9705 - accuracy: 0.6527 - val_loss: 1.1542 - val_accuracy: 0.5895 Epoch 8/10 1563/1563 [==============================] - 10s 6ms/step - loss: 0.9291 - accuracy: 0.6695 - val_loss: 1.1680 - val_accuracy: 0.5924 Epoch 9/10 1563/1563 [==============================] - 10s 6ms/step - loss: 0.8837 - accuracy: 0.6884 - val_loss: 1.1302 - val_accuracy: 0.6039 Epoch 10/10 1563/1563 [==============================] - 10s 6ms/step - loss: 0.8437 - accuracy: 0.7029 - val_loss: 1.1593 - val_accuracy: 0.6018
reg_accuracy = reg_history.history['accuracy']
wn_accuracy = wn_history.history['accuracy']
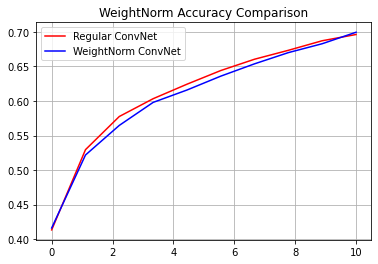
plt.plot(np.linspace(0, epochs, epochs), reg_accuracy,
color='red', label='Regular ConvNet')
plt.plot(np.linspace(0, epochs, epochs), wn_accuracy,
color='blue', label='WeightNorm ConvNet')
plt.title('WeightNorm Accuracy Comparison')
plt.legend()
plt.grid(True)
plt.show()